Does the central nervous system impose biased representations on cognition?

Harry Howard

Tulane University

1. Introduction to linguistic age/gender biases

Natural language is rife with asymmetries that belie a biased or ideological world view. This paper argues that such biases are the result of where prototypes are located on scales of measurement. The scales discussed in this paper are those used for the classification of people in terms of age and gender in certain morphological constructions in English and Spanish.

1.1. Man/other asymmetries

Perhaps the clearest case is the usage of the word man to refer to the whole human species. One can distinguish four varieties: (a) generic contexts, (b) certain collective, distributive, and possessive phrases, (c) through compounding with other parts of speech, and (d) as a verb. These are exemplified in (1):

(1)

a.

Man is the measure of all things.
Man hopes for peace, but he prepares for war.

b.

When the audience smelled smoke, it was every man for himself.
They arose as one man to protest the verdict.
After a refreshing sleep, he was again his own man.

c.

man-eater "an eater of humans"
manhandle "to move by human strength, without mechanical force"
manhole "a hole through which humans enter a sewer, drain, etc"
mankind "humanity"
man-made "made by humans"
man-hour "the work done by a human in an hour"
manhunt "an intensive search for a human that has run afoul of the law"
manpower "work performed by a number of humans"
manslayer "a killer of humans"
manward "towards humanity, as opposed to towards God or heaven"

d.

to man "to furnish with human workers"

There are several other instances of (1c) found in specialized nautical, industrial, or military terminology.

1.2. Masculine/feminine asymmetries

One of the best-known examples is that grammatical devices associated with male gender have broader reference than those associated with female gender in many western European languages.

In English, the principle manifestation of this asymmetry is the usage of the pronoun he for referents of mixed or unknown gender. There are two cases: (a) the bound-pronoun reading, in which the pronoun is in the scope of a quantified noun phrase, and (b) headless relative clauses:

(2)

1. Everyone_i said that he_i had a good time.
2. He who hesitates is lost.

Both usages of he include reference to girls and women. Conversely, replacement of he with she does not rule in reference to boys or men.

Spanish has a highly productive system of masculine-feminine contrasts in grammatical gender for humans and other animals, as exemplified in Table 1:

Tío and gato are masculine, as signaled by the word-final 'o', while tía and gata are feminine, as signaled by the word-final 'a'. In most usages, the morphological gender of animals corresponds to their natural gender. However, the masculine gender can be used to refer to the female sex in certain special contexts. The three most common are (i) situations in which the sex of the animal is unknown, (ii) generic reference, and (iii) in the plural for groups of mixed sex.

As an example of the first, consider a situation in which a cat is recognized from a distance by its silhouette, but it is too far away to ascertain its sex. Any discussion about it must perforce be conducted using the masculine gender:

(3)

¿Qué es aquello? - Es un gato.
what is that? - [it] is a cat-m

Generic reference is reference to the general notion of the animal:

(4)

El gato es cazador nato de ratas.
the cat-m is hunter born of rats
'The cat is a born rat-hunter.'

The masculine plural form can refer back to mixed sexes. Imagine (5a) as a statement and (5b) as a question about the cats introduced in (5a):

(5)

a. Tengo una tortuga, un perro, un gato y una gata.
I-have a turtle, a dog, a cat-m and a cat-f
b. ¿Dónde están los gatos?
where are the cats-m

In all three cases, substitution of the feminine gender for the masculine changes the reference to exclusively female cats.

A third instance of morphology with a specific gender reference is constituted by those morphemes that turn a stem denoting humans or other animals into the corresponding female. English has at least two such morphemes, the suffixes -ess and -ine, exemplified in Table 2:

1.3. Adult/child asymmetries

English and Spanish also betray certain asymmetries between reference to adults and reference to children, giving preference to the former. Two morphological phenomena are reviewed below, English age/gender suffixes, which turn out to be inconclusive, and diminutives in English and Spanish.

1.3.1. English age/gender suffixes

English has a fairly productive system of noun compounding in which the four age/gender terms - plus two others - become destressed suffixes to a noun stem. I say that it is fairly productive, but a glance at Table 3 shows it be productive mainly for adult terms:

However, there is one point that may indeed reflect a property of English - the first two lines consisting of kins- and English-. The child-based compounds are ill-formed and are included in the adults. For instance, in the children's story "Jack and the Beanstalk", the giant is famous for yelling "Fee, fie, fo, fum, I smell the blood of an Englishman!" when he is in fact smelling the blood of a English boy, Jack. Since there appears to be no pragmatic reason why my five-year-old niece is not my kinsgirl or why the young son of my Welsh friends is not a Welshboy, I conclude that the adult forms include the child forms in these two cases.

1.3.2. Diminutives

More straightforward is the data from diminutive formation. There is a suffix /i/ in English that when added to a proper name of the proper phonological form converts it into a name suitable for a child:

The conclusion is clear: the adult sense is unmarked, while the child sense is marked by the diminutive. It follows that we are once again faced with a case of bias by inclusion, in that the adult form includes covert or implicit reference to the child that is brought out by the diminutive, but the child form does not include any reference to the adult at all.

2. Introduction to the age/gender data object

2.1. A space for English age/gender terms

As a first step towards illustrating this outcome for natural language, let us assume that the meaning of a singular or plural noun is based on a pattern of observations of individuals who instantiate the noun. Take as an example the English count nouns man, boy, girl, and woman. Their denotations are composed of values for at least two parameters, AGE and GENDER, as laid out in Table 6:

Note that for the parameter AGE, we can be very precise. In the social research literature, it is standardly measured on a ratio scale, which is a scale from zero to some maximal value that supports all of the operations of ordinary arithmetic. For ease of exposition, 'one' is chosen here as the maximal value, under the interpretation that it stands for the age of 100. With this interpretation in hand, the threshold for 'young' can be fixed at, say, 0.2 or 20 years old.

As for GENDER, in the social research literature, it is standardly measured on a nominal scale, vid. inter alia Healey (1996:12-3), which means simply that it is category for which one can count individual instances but cannot make any further arithmetic determinations. Though accurate, for our cognitive linguistic purposes, such an ordinal scale is not precise enough to describe how individuals are assigned particular age/gender labels. In particular, it does not provide enough detail to understand the transition from the child to the adult categories. A girl is not just a young woman, that is, a person with all of the female properties of a woman except for a certain age, but rather a person that lacks some of the female properties of a woman and can only gain them through experience or some other aspect of the maturation process - and may not gain all of them ever. Mutatis mutandis, the same holds for the boy/man distinction.

Such reasoning implies that GENDER should at least be described by an ordinal scale, which permits relative determinations of "less than" or "greater than", so that the scale can show that a girl has a lower score on it than a woman, and a boy a lower score than a man. Building in the full power of a ratio scale may not be necessary, however, since I at least find it difficult to imagine a situation in which one would want to claim that "a woman is twice as female as a girl", or something to that effect. Yet for the adult categories, this may not be so far-fetched. English certainly supports such locutions as "he is twice the man you are". Moreover, there appears to be a prototypical MAN that lies somewhere between the hyperbolic MACHO and SISSY terms on a scale of masculinity.

Thus our decision is to measure GENDER on a scale that supports at least ordinal differentiations. However, determining the end-points of such a scale is no easy matter, because any choice imposes biases on the resulting system. In the rest of this section, we review three end-points, (i) female-male as [0, 1], (ii) female-male as [-1, 1], and (iii) female-male-female as [-1, 1], and ascertain which one provides the best account of the age/gender distinctions outlined above.

Our first choice is to assume a scale of GENDER from 0 to 1, where 0 is the least female, that is, the most male, and 1 is the most female. For the sake of explicitness, let us assume that GENDER is divided into quarters. Neuter lies along the imaginary line defined by GENDER = 0.5. A set of ten made-up observations that instantiate these terms is set forth in Table 7:

o = MAN, * = BOY, x = GIRL, + = WOMAN

Figure 1. Observations of AGE x GENDER with female maximum at 0

The third dimension, the unlabeled z axis, is not used here, but it is included to maintain consistency with upcoming graphs.

An alternative conception of the gender parameter can be found by assigning male and female to the maxima of 1 and -1, respectively. A plot of a population of 271 individuals fulfilling this criterion is given in Fig. 2:

o = MAN, * = BOY, x = GIRL, + = WOMAN

Figure 2. Observations of AGE x GENDER with female maximum at -1

The ideological claim of the new representation is that male and female are equal though opposite extremes, separated by a neutral zone which lacks any distinguishing male/female characteristic.

A third possibility combines the other two. Like the first, it situates male at the unmarked value of 0 on a scale of gender, and like the second, the scale has two symmetric poles at -1 and 1. The difference is that female gets assigned to both polarities, as illustrated in Fig. 3:

o = MAN, * = BOY, x = GIRL, + = WOMAN

Figure 3. Observations of AGE x GENDER with female maxima at -1 and 1

The result is that male observations clump up along the gender centerline at 0, while female observations spread out along the two edges.

2.2. Which model is best?

The next step is to ascertain which of the three representations of gender constructed above provide the best account of the morphological data under consideration. We argue that the second is best, mainly by excluding the first and third.

The first scale of gender lies in the interval [0, 1], where 0 is the least female, that is, the most male, and 1 is the most female. This scale encodes in the most direct way imaginable that male is unmarked (max = 0, e.g. he is the default pronoun in English), and female is marked (max = 1, e.g. derivation of female nouns from male nouns plus a morphological marker in English). However, there is one counterintuitive result: both of the male classes are partially female. Men can be up to 25% female, while boys can go as high as 50%. Even the prototypical MAN is 15% female, vid. Table 4. Such percentages contradict the assumption that male is unmarked and suggest that the interval [0, 1] is not the best scale for gender.

Turning to the third format, the scale of gender lies in the interval [-1, 1], where 0 is the least female, that is, the most male, and both -1 and 1 are the most female. The ideological claim of this representation is that male rests in the neutral ground between two female extremes, which is tantamount to claiming that there are two female genders. This may seem at first glance to be a counterfactual assertion, but the issues raised in Nesset's paper shows that it does indeed play an important role in gender-based reasoning. In fact, such a representation grounds Nesset's discussion of the VIRGEN-WHORE polarity as developed by de Beauvoir. The crucial difference is that this dichotomy no longer answers to a scale of gender, but rather something more akin to morality. Unfortunately, such considerations take us beyond the strictly linguistic purview of this paper, so I simply conclude that the third format is a good idea, just not the best one for the rather limited notion of gender in play here.

Given that the only one left standing is the second scale, the one in the interval [-1, 1], where -1 is the most female, and 1 is the most male, it follows that we have proved by exclusion that the second scale is the best for our data. We hasten to add that no justification has been adduced for the choice of which extreme to assign to which gender - an issue that is addressed more fully at the end of the paper.

2.3. Advantages of this representational format

There are several advantages to grounding the meaning of age/gender terms on these kinds of numerical considerations. Perhaps the main one is that they let us define Cognitive-Linguistic notions in a precise manner without assuming an objectivist metaphysics. The next few subsections amplify on this claim by exploring how cognitively interesting categories can be defined on the basis of the correlations found in AGE x GENDER.

2.3.1. The calculation of prototypes

The rich mathematical structure of any structure like the AGE x GENDER space provides several ways to define the notion of a prototype familiar from cognitive psychology, vid. Rosch (1973, 1975, 1978), Mervis & Rosch (1981) and much posterior research. There are two alternatives, which depend to a large extent on the statistical properties of the model.

If the distribution of observations is uniform, then a simple choice is to define a prototype as the centroid of the observations making up a category, such as their arithmetic average:

(6) prototype = sum of observations/number of observations

Note that the prototypical individual so-defined need not coincide with an observed individual.

In contrast, if the distribution of observations is normal, an additional possibility presents itself. That is to define the prototype as the area with the highest number of observations, which is equivalent to defining it as the place where values of the different parameters tend to cluster. Since by 'cluster' we mean 'are highly correlated', it follows that a cognitive prototype is an area of high correlation among the semantic features that define the category.

This notion of correlation between features finds a neurologically-plausible implementation in the notion of Hebbian learning. Hebbian learning is a hypothesis of how neurons change under the influence of experience. It is attributed to Hebb (1949), where the following postulate is made:

When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased.

Slightly more succinctly, Hebb's postulate says that if the firing of cell A correlates with the firing of cell B, then the synapse between them will change so as to enhance the effect of A on B.

This sounds very much like the notion of feature correlation just mentioned, except that in the latter case, three cells are involved. Fig. 4 diagrams what I have in mind:

Figure 4. Hebbian correlation between AGE and GENDER

Assume that cell A represents the value of AGE that has the most instances and that cell A' represents the value of GENDER that has the most instances. Both of them will fire repeatedly in tandem to fire cell B. If the connections from A and A' to B undergo Hebbian strengthening, so that A and A' become the cells that B preferentially responds to, then cell B will come to represent the individual with coordinates [A, A'] in AGE x GENDER. In fact, given the assumption that [A, A'] is the most frequent observation in AGE x GENDER, cell B will come to represent the prototype for this particular group of observations.

In mathematical terms, Hebb's postulate can be understood to claim that a synapse can be represented by a (real) number whose value increases if the two cells on either side of it are correlated. Fig. 5 displays the results of applying a version of this algorithm to the data of Fig. 2. The 'floor' or baseline of zero correlation is set arbitrarily to a small positive value, here 0.05, to represent the value that all cells have before being exposed to the age/gender population. The peaks above this floor mark spots of Hebbian correlation. The higher the peak, the higher the correlation:

Figure 5. Hebbian correlation between AGE and GENDER

It is hoped that the reader can discern the clusters of peaks that define the prototypes for each age/gender term.

2.3.2. 'Goodness of fit' to a category

Having such a nuanced hypothesis of the representation of prototypes allows us to define several ancillary notions. The most useful is that of an individual's 'goodness of fit' to a category, which can be calculated by measuring the gap between the individual and the prototype.

For instance, Fig. 6 uses arrows to depict distances between a prototype and a specific observation:

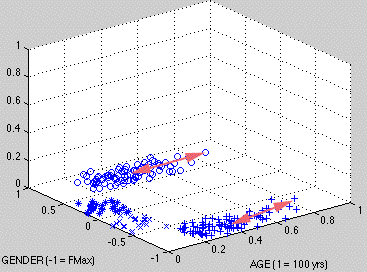
o = MAN, * = BOY, x = GIRL, + = WOMAN

Figure 6. Measurements between prototypes and sample individuals

Clearly, though, what we want to know is the measurement between a prototype and all of its points on the AGE x GENDER plane.

However, the reader may have detected an ambiguity in the phrasing of this discussion. I have carefully avoided choosing between saying that what needs to be measured is the distance from the prototype to the individual or the nearness of the prototype to the individual. The reason for this ambiguity is mathematical: distance and nearness are inverses of each other and so lead to quite different conceptualizations of relationship between individuals and their prototypes. By way of illustration, consider the following table:

Figure 7. NEARNESS vs. DISTANCE to prototypes in AGE x GENDER

2.3.3. Hyperbolic prototypes

Not does the AGE x GENDER plane the calculation of the 'normal' prototype, it also supports the definition of several hyperbolic prototypes as the maximum distance from the normal prototype. Fig. 8 points out three obvious male ones:

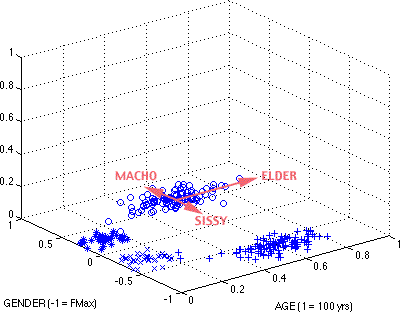
o = MAN, * = BOY, x = GIRL, + = WOMAN

Figure 8. MAN hyperbolic prototypes

Putting the picture into words, the claim is that the MACHO hyperbolic prototype has the maximum value for male along the gender axis from the MAN prototype, while the SISSY hyperbolic prototype has the minimum value. Along the age axis, the (male) ELDER hyperbolic prototype has the maximum value from the prototype. Of course, there is also a minimum value in the opposite direction, but I could not find a suitable term for it in English. All of the contenders appear to be coopted by BOY.

2.3.4. Comparisons to Montague Grammar

As an aside, it should be pointed out that three other results show the way to an account of Montague Grammar concepts that again does rely on objectivist presuppositions. First of all, the notion of a potential individual can be defined as an individual within the cluster of observations that does not correspond to an observed individual. This effect provides us with the basis for a possible-worlds semantics that does not rely on possible worlds. Secondly, the extension of a category is simply defined as the set of all observed individuals. Finally, the intension of a category can be defined as the entire space of the cluster, which includes the observed, possible, and prototypical individuals. Note that this geometric definition of intension is inherently functional or relational, in that it delimits where the category fits into the larger space of nearby categories. For instance, knowing where the subspace of BOY is in any of the figures above tells you how BOY relates to its neighboring subspaces of MAN, GIRL, and WOMAN.

3. A receptive-field account of age/gender biases

Let us examine the measure of NEARNESS to a prototype without reference to the underlying statistical model, for instance, by plotting the nearness of every point in a category to its prototype:

Figure 9. NEARNESS to all prototypes in AGE x GENDER

A point that sits atop its reference point, or whose reference point is itself, takes on the highest value for NEARNESS, here set arbitrarily to 1. This value falls as the point is displaced from its reference point. The colors in Fig. 9 shift from warm to cool in step with this transition from near to far away, as depicted by the numbered bar on the right. The net effect of this graph is to cull the NEARNESS information out of Fig. 7 for independent inspection.

Moreover, Fig. 9 looks astonishingly like a positron emission tomographic image of the brain, magnified to show the activity of a specific region.

Let us take a page from neurophysiology, for instance, from Delcomyn (1998:222), and call the concentric area of graded NEARNESS around a prototype the receptive field of the prototype, on a par with the receptive fields of sensory neurons. In a sensory neuron,

The region or area of a sensory surface that must be stimulated in order to elect a change in activity in a neuron is called the neuron's receptive field.

Of course, our initial guess is that a representation like Fig. 9 encodes a multitude of neurons, if not an entire cerebral column or more, but the idea remains the same. Just so there is no misunderstanding, let me clarify what the idea is: the closer a stimulus is to a prototype on the sensory surface of AGE x GENDER, the stronger will be the ensemble's response to the stimulus.

With the equation of AGE x GENDER to a sensory surface, and the prototypes found thereon to a receptive field, I now have a sophisticated enough apparatus to formulate the hypothesis of the paper: the various age/gender phenomena considered above can be accounted for by some combination, weakening, or strengthening of the four receptive fields shown in Fig. 9.

3.1. MAN/other asymmetries as inclusive man

The first step is to isolate a single receptive field, such as the one organized around the prototype for MAN:

Figure 10. NEARNESS to MAN in AGE x GENDER

The mathematical interpretation of this graph is that the input of an observation of a man, say at <0.5, 0.7>, produces an output of about 0.85, while the input of an observation of a woman, say at <0.5, -0.6>, produces an output of about 0.05. Assuming that the outputs lie in the interval [0, 1], 0.85 indicates a strong response to the prototypical man, while 0.05 indicates a very weak response. The cognitive interpretation is that the system recognizes <0.5, 0.7> as a good instance of a man, and <0.5, -0.6> as a very bad instance of one. Since the other three prototypes organize their surrounding space in an equivalent way, I claim that this system constitutes a first approximation to a neurologically-inspired theory of age/gender contrasts.

The usage of man to refer to all of humanity can be accounted for by bringing in the other three prototypes at slightly reduced values. Fig. 11 depicts what I have in mind:

Figure 11. NEARNESS to MAN+ in AGE x GENDER

This sensory surface still responds most strongly to men, but it also responds in an attenuated fashion to the other three age/gender classes. This special asymmetric variation in the sensory surface will be referred to by superscripting a '+' to the dominant receptive field, here giving MAN+. Note that MAN+ can be called inclusive, since it includes sensitivity the other three receptive fields, while MAN should be called exclusive, because it does not.

In this way, we can account for the conflict between the prescriptive and the feminist intuitions about the biased usage of man. From the prescriptive perspective, the usage of man to refer to all of humanity is equivalent to a second sense for man - a neutral one that does not unduly prejudice against any other age/gender category. From the feminist perspective, this usage of man does exclude the other three categories. The difference lies in differing appreciations of the unequal weighting of the four receptive fields: the prescriptivist gives more play to the fact that all four categories are active to a certain extent; the feminist, to the fact that MAN is more active that the others.

3.2. Masculine/feminine asymmetries as inclusive MASCULINE

My account of the data on contra-female bias takes the preceding discussion one step further by introducing the notion of a complex prototype, which is simply a collection of basic prototypes.

3.2.1. Exclusive vs. inclusive masculine gender

Consider what masculine gender would look like in this system - namely, Fig. 12:

Figure 12. NEARNESS to MASCULINE in AGE x GENDER

What we see are two zones of high response, which I claim are combined to form a single complex receptive field making up the representation of masculine gender. Note crucially that this field gives a minimum response to the female half of the sensory surface.

The means of generalizing this representation to the usage of masculine gender to refer to all people is just as before: the missing half of the range is brought in at a lower response level, as in Fig. 13:

Figure 13. NEARNESS to MASCULINE+ in AGE x GENDER

This surface now responds to both males and females, though its response is higher to males. It once again models quite accurately the prescriptivist and feminist reactions to using male gender for reference to females, which are no different in substance from those discussed at the end of the previous subsection.

3.2.2. Feminizing morphology

This proposal does not account for morphology that converts masculine nouns to feminine ones, at least not without further elaboration. If Fig. 13 can act as a template for all grammatical gender assignment, then the global result for the nominal system is that it will respond preferentially to masculine, while some sort of conversion process is required to turn Fig. 13 into its feminine counterpart of Fig. 14:

Figure 14. NEARNESS to FEMININE in AGE x GENDER

I claim that this conversion is accomplished by feminine suffixes in English. It follows that the optimal route to create female nouns is by morphological addition to male nouns. Note that it will not do to try to derive male nouns by morphological 'subtraction' from a more complex female noun, because the FEMININE surface of Fig. 14 has no sensitivity to males, so there is no way to know where the male prototypes are in the empty top half.

3.3. Adult/child asymmetries as inclusive ADULT

By now, the account to be proposed for the English age/gender compound nouns and the English and Spanish diminutives should be recognizable as a simple generalization of the previous accounts to the vertical orientation of the AGE axis. The ADULT+ field reflected in the unmarked forms includes CHILD at lower levels of activation, vid. Fig. 15, while the CHILD receptive field reflected in the marked forms excludes the ADULT half of the field, vid. Fig. 16:

Figure 15. NEARNESS to ADULT+ in AGE x GENDER

Figure 16. NEARNESS to CHILD in AGE x GENDER

Thus contra-child biases can be assimilated to the system that underlies the other types of bias discussed in this paper.

4. Which alternative is chosen to be inclusive?

The crucial remaining question is how a prototype is chosen to be inclusive. By Occam's razor, it would be more economical to find a motivation within the system than beyond it, so we would like to know whether this framework is rich enough that bias springs automatically from its neurolinguistic constitution, or whether bias is imposed on it by some external, presumably cultural, factors.

4.1. The asymmetry of [0, 1] scales

The many philosophers and psycholinguists who have studied negation have concluded that negative inferences are marked with respect to positive ones, vid. Horn (1989:§3) for a recent review. As one illustration of this asymmetry, consider how + Adj. questions, in which the most felicitous form of an adjective is the one without the corresponding un- or in- prefix:

(7)

1. How {frequent/#infrequent} is rain in the Sahara?
2. How {important/#unimportant} is a janitor in your company?
3. How {possible/#impossible} is it to square a circle?
4. How {likely/#unlikely} is it that you will win the lottery?
5. How {popular/#unpopular} was the President during his last sex scandal?

On the one hand, despite the fact that the more felicitous forms denote at the high end of their scale, all of these questions can be answered with a low-end expression, such as Not very X, Not at all X, or Not as X as I would have liked. On the other hand, the crosshatched forms only become felicitous if their proposition has already been asserted, e.g.:

(8)

1. ME: The President was not very popular during his last sex scandal.
2. YOU: So, just how unpopular was he?

What adds more significance to this fact about negative forms is the observation of Givón (1970) that the preferred form of how + Adj. questions takes the 'larger' or monotone increasing value in a multitude of common cases:

(9)

1. How {many/#few} cupcakes do you have?
2. How {much/#little} logic do you know?
3. How {tall/#short} is the baby?
4. How {long/#short} is your fingernail?
5. How {old/#young} is the baby?
6. How {heavy/#light} is a balloon full of helium?
7. How {fast/#slow} does a snail crawl?
8. How {strong/#weak} is an ant?
9. How {high/#low} is the first step?
10. How {deep/#shallow} is the puddle?
11. How {wide/#narrow} is a hair?
12. How {often/#seldom} does it rain in the Sahara?
13. How {far/#near} can you see without glasses?
14. How {tight/#loose} did you tie your shoelace?
15. How {full/#empty} is your glass?
16. How {loud/#soft} is the wind?
17. How {different/#similar} is your twin?
18. How {rich/#poor} do you have to be to qualify for Welfare?

Again, the crosshatched alternatives are only felicitous if their proposition has already been asserted, e.g.:

(10)

1. ME: I have very few cupcakes to give away today.
2. YOU: So, how few cupcakes do you have?

This asymmetry is reproduced in the nominal domain. If the name of the scales exemplified above is derived from an adjective, the adjective is the maximal one:

(11)

1. frequent/infrequent > What is the {frequency/#infrequency} of rain in the Sahara?
2. important/unimportant > What is the {importance/#unimportance} of a janitor in your company?
3. possible/impossible > What is the {possibility/#impossibility} of squaring a circle?
4. likely/unlikely > What is your {likelihood/#unlikelihood} of winning the lottery?
5. popular/unpopular > What was the {popularity/#unpopularity} of the President during his last sex scandal?

(12)

1. long/short > What is the {length/#shortness} of your fingernail?
2. strong/weak > What is the {strength/#weakness} of an ant?
3. high/low > What is the {height/#lowness} of the first step?
4. deep/shallow > What is the {depth/#shallowness} of the puddle?
5. wide/narrow > What is the {width/#narrowness} of a hair?
6. loud/soft > What is the {loudness/#softness} of the wind?
7. different/similar > What is the {difference/#similarity} between you and your twin?

My tentative conclusion is that the asymmetry of all of these antonymic pairs can be assimilated to the receptive field proposed for the ADULT+ prototype above, in which the high end of the scale of AGE includes the low end, but not vice versa.

This result undoubtedly has a much wider reach than the smattering of data adduced here. For instance, if we make the assumption that the prototypical state of an entity lacks defects, then the choice between a number of adjective antonyms in how + Adj. questions is resolved in favor of the one that denotes the higher degree of defectiveness:

(13)

1. How {crazy/#sane} is the inmate?
2. How {sick/#well} is the patient?
3. How {broken/#whole} is the vase?

Unfortunately, this is not the place to undertake a comprehensive investigation.

Such considerations embolden me to hazard the following conjecture:

(14) Magnitude conjecture: The higher end of a scale, [0.5, 1], is more salient than the lower end, e.g. [0, 0.5].

Under the supposition that inclusive prototypes must be inherently salient to the human cognitive system, the theorem below follows naturally:

(15) Inclusive prototype theorem: An inclusive prototype is preferentially located in the more salient end of a scale in [0, 1].

Given that the rest of the space is evaluated in terms of distance from the prototype, the overall conclusion is that the axes of a space impose subtle biases on the phenomena represented within it.

4.2. [-1, 1] scales and vector-space ontology

What about [-1, 1] scales? The short answer is that -1 is less than 1, so the '1' end of a scale in [-1, 1] should also be the locus for inclusive prototypes, a prediction that abundantly supported by the results for the MAN+ and MASCULINE+ prototypes.

Despite the seductiveness of such an easy answer, it should be regarded with considerable skepticism. The problem is that the negativeness of the half of the scale from 0 to -1 expresses an orientation away from neuter 0 that is lost if the scale is treated just as a set of magnitudes. That is to say, females are not just males with a smaller magnitude of some gender measurement; females are people with the same magnitude for the measurement, but in the opposite direction. Mathematically, what is needed is to treat the points of AGE x GENDER as vectors.

A vector is an ordered string of numbers, each of which specifies the value of a particular attribute, e.g. <2, 7>. The requirement of ordering means that position in the string matters: <2, 7> is not equivalent to <7, 2>. Such strings have a natural geometric interpretation as directed line segments in a coordinate system. A directed line segment is a line with a magnitude (its length measured from the origin) and a direction (its angle from the origin). Fig. 17 shows the geometric interpretation of the vectors <0.5, 0.5> and <0.5, -0.5>:

Figure 17. Geometric interpretation of two vectors

Note that the positive quadrant of the y axis is oriented between 0° and 90°, while the negative quadrant is oriented between 270° and 360°. This difference in angle is what differentiates the two points, since they are displaced to the same magnitude from the origin. The measures of distance from a prototype are all vectors, and the two-dimensional space AGE x GENDER that contains them is a vector space.

Vectors are the natural data structure for the fundamental information-processing behaviors of the central nervous system, and a vector-space ontology of cognitive science has already been developed in Churchland (1986), Gallistel (1990, §14), Churchland & Sejnowski (1992) among others. It follows that the analysis of age/gender bias assayed above is firmly grounded in general properties of the human cognitive system.

Of course, if a vector-space ontology is adopted, we lose the simple magnitude-based explanation sketched in the first paragraph of this section for why inclusive prototypes are found in the positive half of [-1, 1]. Actually, it is more accurate to say that the magnitude-based explanation becomes symmetric. In mathematical convention, the quantity of a number irrespective of its sign is known as its absolute value, indicated by putting the number between bars, |n|. It follows that the principles in (14) and (15) need to be revised along the lines of (16) to refer to absolute, not relative, values:

(16)

1. Magnitude conjecture (revised): The higher end of a scale, |[0.5, 1]|, is more salient than the lower end, e.g. |[0, 0.5]|.
2. Inclusive prototype theorem (revised): An inclusive prototype is preferentially located in the more salient end of a scale in |[0, 1]|.

Given that the WOMAN prototype is located in the higher end of its scale of GENDER, the revised inclusive prototype theorem no longer accounts for why WOMAN does not act as an inclusive prototype on a par with MAN, or even in place of it.

Before appealing to cultural influence, let us make one last stab at a neuromimetic account. In particular, we would like to know whether any asymmetry inheres to the negative y axis, or more accurately, to the points that share its orientation, due solely to that orientation. The main possibility is that the negative half of the axis is encoded by neurons whose output is inhibitory, as opposed to the excitory output of the putative neurons of the positive half. In the mathematical modeling of neurological ensembles, the excitory/inhibitory contrast is quantified exactly in the terms that we have been using: excitation is modeled as a positive number, and inhibition is modeled as a negative number, so that the summation of the two in equal magnitudes cancels out to zero.

It follows that if there is any asymmetry in the properties of excitation and inhibition, then it should be reflected in the cognitive processes which they subserved. Actually, one can gain inklings of such an asymmetry in the general assumption that neurological activation, that is, the sum of excitation and inhibition, tends to be positive. Again, painting in very broad strokes, the general layout of the brain is of few excitory neurons embedded in the midst of many inhibitory neurons in such a way that the excitory neurons exchange excitation to the extent that it overcomes the surrounding inhibition. Thus, in an impressionistic sense, excitation can be taken to be more active than inhibition. This intuition supplies the shaky foundation on which to build the conjecture in (17a) and revise the inclusive prototype theorem to (17b):

(17)

1. Orientation conjecture: The positive half of a scale, [0, 1], is more salient than the negative half, [-1, 0].
2. Inclusive prototype theorem (revised): An inclusive prototype is preferentially located in the more salient half of a scale.

This revision of the theorem now accounts for all of the data: (i) MAN+ is inclusive because it has both the most salient magnitude and the most salient orientation; (ii) MASCULINE+ is inclusive because it has the most salient orientation; and (iii) ADULT+ is inclusive because it has the most salient magnitude.

It may now appear to the reader that we have derived the three age/gender linguistic asymmetries independently of any input from the encompassing cultural system, but this appearance is deceptive. Since the exact perceptual basis of the GENDER orientation has not been defined, it is exceedingly likely that the axis itself is a cultural phenomenon. In fact, I think that this is the real moral of the story: it is not that the neurolinguistic system developed here biases the language learner towards male and away from female, but rather that the system encourages the language learner - if not the culture learner - to synthesize ternary categories organized into two poles around a neutral center, in which one pole is dominant and the other recessive. For such categorization to be successful, there must be enough clues in the linguistico-cultural context for the learner to discover the underlying orientation, and the linguistic data reviewed above suggest that English and Spanish supply more than enough.

As a final note, the reader may be tempted to come away form her reading of this paper with a feeling of pessimism about the possibility of ever achieving a bias-free society, since bias appears to be an inescapable ingredient of human cognition. Nevertheless, what has been overlooked so far in the model is the time course of processing. Age/gender bias has been examined as a perceptual/categorizational phenomenon, and it is well known that such phenomena are processed at an extremely fast rate, on the order of a few hundred milliseconds. It is also well known that there is a posterior stage of 'reflective thought' or something similar, which proceeds at a more leisurely pace of seconds to minutes. It is at this second stage that an individual's entire store of knowledge can be brought to bear on age/gender issues and so neutralize or reverse the outcome of the automatic initial perceptual/categorizational bias - if the individual is so-inclined.

5. Some thoughts on Nesset

Nesset's characterization of the Russian a-declension has several points of comparison with the phenomena and analysis outlined above. To refresh the reader's memory, Nesset finds that the Russian a-declension marks (i) female people, (ii) nouns that mark intimate relations, such as the short form of names, terms for family relations, and terms of address between intimates, and (iii) common nouns that denote entities that occupy the margins of their category. Nesset argues that the latter two belong to the schema of FAMILIARITY and MARGINALITY, which can be subsumed with (i) under a more general schema of NON-PROTOTYPICALITY, under the assumption that women are the "second sex".

These schema are obviously scalar entities, a fact which Nesset acknowledges at several points. As such, they should have a ready instantiation in the scales of measurement used here. Fig. 18 sketches a first approximation, which abstracts from most of the details of implementation and only attempts to portray the principle binary distinctions in play, plus the metaphors that motivate the associations between categories:

Figure 18. Three maps of the Russian a-declension

I believe that this format preserves the essential insights of Nesset's analysis, while having the advantages of greater mathematical rigor and neurological grounding.

Where the frameworks differ is in the amount of conceptual material that has to be stipulated separately. For instance, there is no need to mention the superschema NON-PROTOTYPICALITY in Fig. 18, because it is implicit in the biased structure of the scales. That is, the blue halves are assumed to house an inclusive prototype for each map, so there is no need to stipulate NON-PROTOTYPICALITY separately. In a similar vein, there is no reason to stipulate 'woman as the second sex' in the gender map, since this bias is already implicit in the scale. It may even be redundant to name the associations between the maps, indicated by arrows in Fig. 18, since there is enough information in the maps themselves to indicate the correct alignment. Such simplifications are welcome, since they help to bring out the proper level of generalization and rid the theory of otiose concepts and mechanisms.

6. Summary and speculation: why are there no ugliness contests?

To summarize briefly, this paper attempts to account for asymmetries in the usage of age and gender morphology in English and Spanish by a three-step process: postulate a statistical model that approximates the distinctions to be learned, (ii) find correlations among the parameters of the model, and (iii) define the areas of highest correlation as prototypes. It turns out that the asymmetries in the application of age/gender morphology can be accounted for in terms of nearness to the prototypes elucidated in this process.

This process should have a much broader zone of application than just age/gender morphology, and I would like to end the paper on a more speculative note, concerning what these further areas might look like.

Consider for a moment how appearance is conceptualized. In common language, there is obviously a scale for valuation, which goes from a low of 'ugly' to a high of 'beautiful', passing through a neutral middle ground of 'plain'. If this valuation were symmetric, a high degree of beauty would entail a low degree of ugliness, and vice versa. In fact, if the valuation were symmetric, humans would engage in 'ugliness contests' with the same probability that they engage in beauty contests. Under symmetry, there are two ways of ranking contestants: the winner of a beauty contest is the one who accumulates the most 'beauty points', and the winner of an ugliness contest is the one who accumulates the fewest 'ugliness points'. The two are mathematically equivalent, so Miss Universe could go either way.

However, by now it should be clear why humans apparently do not readily entertain a notion of beauty as a low score on ugliness. It follows directly from the asymmetry in where prototypes are located on the underlying scale. Beauty presumably constitutes the inclusive prototype on the scale of appearance - and ugliness the exclusive prototype - so that even with an extremely low score of ugliness, the label of 'ugliness' itself still stands as an absolute lack of beauty - and a description that the contestants would presumably not wish to compete for.

7. References

Churchland, Patricia Smith. 1986. Neurophilosophy. Toward a Unified Science of the Mind-Brain. Cambridge, USA & London, England: The MIT Press.

Churchland, Patricia Smith & Terrence Sejnowski. 1992. The Computational Brain. Cambridge, Mass.: The MIT Press.

Delcomyn, Fred. 1998. Foundations of Neurobiology. New York, NY: W. H. Freeman and Co..

Gallistel, C. R. 1990. The Organization of Learning. Cambridge, Mass.: MIT Press.

Givón, Talmy. 1970. Notes on the Semantic Structure of English Adjectives. Language. 46:816-837.

Healey, Joseph F. 1996. Statistics. A tool for social research. Belmont, CA.: Wadsworth Publishing.

Hebb, Donald Olding. 1949. The Organization of Behavior. New York: John Wiley & Sons.

Horn, Laurence. 1989. A Natural History of Negation. Chicago, Illinois: The University of Chicago Press.

Howard, Harry (1998) Spanish diminutives and neocognitron-type neural processing. First International Conference of the Asociación Española de Lingüística Cognoscitiva, University of Alicante, Alicante, Spain. May 6, 1998.

Mervis, C. & Eleanor Rosch. 1981. Categorization of natural objects. Annual Review of Psychology. 32:89-115.

Rosch, Eleanor. 1973. On the internal structure of perceptual and semantic categories. In Cognitive Development and the Acquisition of Language, ed. Timothy Moore, New York: Academic Press.

Rosch, Eleanor. 1975. Cognitive representaions of semantic categories. Journal of Experimental Psychology. General. 104:192-233.

Rosch, Eleanor. 1978. Prototype classification and logical classification: the two systems. In New Trends in Cognitive Representation, ed. E. Scholink, 73-86. Hillsdale, NJ: Lawrence Erlbaum Associates.