Does the central nervous system

impose biased representations

on cognition?

Natural language is rife with ideology. One of the best-known examples is the unmarked status of male with respect to female in many western European languages. One manifestation of this asymmetry is the usage of the pronoun he for referents of mixed or unknown gender in English; another is the derivation of female nouns from unmarked nouns, i.e. hostess < host; heroine < hero. This paper argues that such biases are the result of a vector-space representation that the central nervous system imposes on cognition.

As a first step towards illustrating this outcome for natural language, let us assume that the meaning of a singular or plural noun is based on a pattern of observations of individuals who instantiate the noun. Take as an example the English count nouns man, boy, girl, and woman. Their denotations are composed of values for at least two parameters, age and gender, as laid out in Table 1:

Let us say that age is measured on a scale from 0 to 1, where 0 indicates the least age and 1 the greatest (for humans). If we assume that the greatest age is 100, we can rather arbitrarily choose the threshold for 'young' to be 0.2, i.e. 20 years old. This does not seem to impose any particular bias.

However, the choice of representation for gender does. To show how this works, let us begin with the ideological assumption that opened the paper, namely that the presence of male attributes is unmarked (for example, he is the default pronoun in English) and the presence of female attributes is marked (for example, derivation of female nouns from male nouns in English). This can be encoded by assuming a scale of FEMALENESS from 0 to 1, where 0 is the least female, that is, the most male, and 1 is the most female. For the sake of explicitness, let us assume divisions between the each class lie at 0.25. Thus men lie in the interval [0 .25], boys lie in the interval [.26 .5], girls lie in the interval [.51 .75], and women lie in the interval [.76 1], while neuter lies along an imaginary line given by FEMALENESS = 0.5.

With these conventions, we can invent a set of ten observations:

Table 2. Sample observations of English gender terms

Figure 1. AGE x FEMALENESS

o = MEN, * = BOYS, x = GIRLS, + = WOMEN

The third dimension, the unlabeled z axis, is not used here, but it is included to maintain consistency with upcoming graphs.

Fig. 1 encodes quite accurately our initial hypothesis of markedness, but it leads to counterintuitive conclusions. In particular, both of the male classes include a measure of femaleness. Boys can have up to 50% femaleness, while men can have up to 25%. Moreover, consider the femaleness component of the prototypical man. We can assume that the prototypical man is found by the arithmetic average of all of the men, which in this example turns out to be <0.61, 0.15>. Thus, even the male prototype is 15% female - which contradicts the assumption that male is unmarked. Some change in the initial assumptions must therefore be sought.

Let us suppose as our second attempt that gender is composed of equal and opposite poles of male and female, in the interval [-1, 1]. We stipulate - for reasons that will become clear below - that the male maximum lies at 1, while the female maximum lies at -1. Thus neuter occupies the mathematically-plausible middle ground at 0. A plot of 200 such observations chosen at random is given in Fig. 2:

Figure 2. AGE x GENDER

o = MEN, * = BOYS, x = GIRLS, + = WOMEN

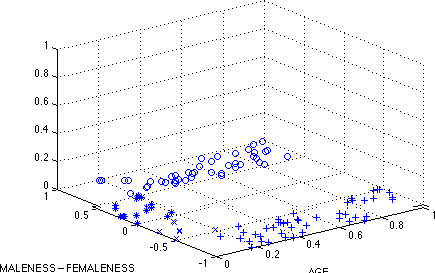
Here we see that maleness and femaleness are given equal status on separate but symmetrical scales.

Given that neither gender is expressed as a deviation from the other, we have lost our explanation for the bias towards male discussed in the first paragraph. Fortunately, an alternative explanation can be constructed from the assumption that the x-y plane supports a measure of distance. The distance that concerns gender bias is the (Euclidean) distance from the male prototype. Three arrows that depict distances to a specific BOY, GIRL and WOMAN observation are given in Fig. 3:

Figure 3. Sample distances from prototype in AGE x GENDER

o = MEN, * = BOYS, x = GIRLS, + = WOMEN; prototype = <0.61, 0.72>

Clearly, though, what we want to know is the distance from the prototype to all of the points on the AGE x GENDER plane. This is plotted onto the third or z dimension, in Fig. 4, which rotates the perspective of Fig. 2 and 3 to give a better view of the GENDER axis:

Figure 4. AGE x GENDER x DISTANCE FROM PROTOTYPE

o = MEN, * = BOYS, x = GIRLS, + = WOMEN; prototype = <0.61, 0.72>

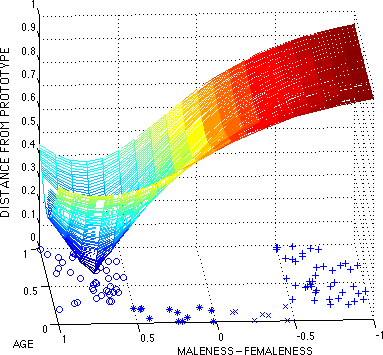
It is hoped that the reader can see a vaguely funnel-shaped manifold overlaying the AGE x GENDER plane, in which the bottom of the funnel touches down on the male prototype. The further a point in AGE x GENDER is from the prototype, the higher is the corresponding point on the DISTANCE axis, up to a maximum of 1.

Fig. 4 supplies us with a simple graphic tool to analyze gender markedness as stability or low-energy. Imagine that the DISTANCE surface in Fig. 4 were a solid physical surface onto which you could put a ball bearing. Given the curve of the surface and the downward tug of gravity, no matter where the ball bearing is placed initially, it will always roll down into the neck of the funnel, on top of the prototype. In physical terms, this is because the higher the point is in DISTANCE, the higher is its energy, and the rolling ball bearing naturally seeks the point of lowest energy. In view of the fact that the ball bearing will stay at the prototype once it gets there, we can conclude that the prototype is the only stable point in the system.

Returning to the linguistic data, if Fig. 4 accurately models the gender of English pronouns, then it follows that the pronominal system will gravitate towards masculine when no more specific choice can be made. Likewise, if Fig. 4 accurately models the gender of English nouns, then the morphological system must put a certain amount of 'energy' into the creation of a feminine noun, whereas no special energy is needed for a masculine noun. It follows that the optimal route is to derive feminine nouns by morphological addition to simpler masculine nouns; or conversely, to derive masculine nouns by morphological 'subtraction' from some more complex feminine noun.

If this simple example generalizes to other ideological domains, then we have a framework for the analysis of bias that is firmly grounded in general properties of the human cognitive system. In fact, such a framework already exists in the form of the vector-space ontology of cognitive science developed in Churchland (1986), Gallistel (1990, §14), Churchland & Sejnowski (1992) among others.

A vector is an ordered string of numbers, each of which specifies the value of a particular attribute, e.g. <2,7>. The requirement of ordering means that position in the string matters: <2,7> is not equivalent to <7,2>. Such strings have a natural geometric interpretation as directed line segments in a coordinate system. A directed line segment is a line with a magnitude (its length) and a direction - both of which are conventionally measured from the origin. Fig. 5 shows the geometric interpretation of the vector <.5, .5>:

Figure 5. Geometrical interpretation of the vector <.5, .5>

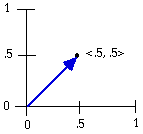
Thus the measures of distance from the prototype in Fig. 3 and 4 are all vectors, and the two- or three-dimensional space that contains them is a vector space.

Vectors are the natural data structure for the fundamental information-processing behaviors of the central nervous system, presynaptic firing frequency and postsynaptic current flow. For instance, the number of action potentials measured per second at a particular axon defines the firing-frequency vector of that axon. It follows that the analysis of gender bias assayed above is embeddable in a more general, neurologically-inspired, cognitive framework.

The crucial remaining question is whether this framework is inherently biased. In particular, we would like to know whether any negative connotation inheres to the negative x axis introduced for FEMALE in Fig. 2. The answer is rather complex and depends on the function of the positive and negative phases of an oscillator in a particular system. However, given that the positive phase of a neural oscillator, or the movement to the peak of the positive phase, is taken to be the 'active' phase, for the sake of falsifiability we can hazard the following conjecture:

Phasal conjecture: The positive half of a scale in [-1, 1] is more salient than the negative half.

Under the supposition that prototypes are somehow inherently salient to the human cognitive system, the theorem below follows naturally:

Prototype theorem: A prototype is preferentially located in the positive half of a scale in [-1, 1].

Given that the rest of the space is evaluated in terms of distance from the prototype, the overall conclusion is that the axes of a vector space impose subtle biases on the phenomenon represented within that space.

BIBLIOGRAPHY

Churchland, Patricia Smith. 1986. Neurophilosophy. Toward a Unified Science of the Mind-Brain. Cambridge, USA & London, England: The MIT Press.

Churchland, Patricia Smith & Terrence Sejnowski. 1992. The Computational Brain. Cambridge, Mass.: The MIT Press.

Gallistel, C. R. 1990. The Organization of Learning. Cambridge, Mass.: MIT Press.