Mineralogy

Prof. Stephen A. Nelson

External Symmetry of Crystals, 32 Crystal Classes

As stated in the last lecture, there are 32 possible combinations of symmetry operations that define the external symmetry of crystals.  These 32 possible combinations result in the 32 crystal classes.  These are often also referred to as the 32 point groups.  We will go over some of these in detail in this lecture, but again I want to remind everyone that the best way to see this material is by looking at the crystal models in lab.  

Hermann-Mauguin (International) Symbols

Before going into the 32 crystal classes, I first want to show you how to derive the Hermann-Mauguin symbols (also called the international symbols) used to describe the crystal classes from the symmetry content.  We'll start with a simple crystal then look at some more complex examples.

The rectangular block shown here has 3 2-fold rotation axes (A₂), 3 mirror planes (m), and a center of symmetry (i).  The rules for deriving the Hermann-Mauguin symbol are as follows:

1. Write a number representing each of the unique rotation axes present.  A unique rotation axis is one that exists by itself and is not produced by another symmetry operation.  In this case, all three 2-fold axes are unique, because each is perpendicular to a different shaped face, so we write a 2 (for 2-fold) for each axis

2   2   2

2. Next we write an "m" for each unique mirror plane.  Again, a unique mirror plane is one that is not produced by any other symmetry operation.  In this example, we can tell that each mirror is unique because each one cuts a different looking face.  So, we write:

2 m 2 m 2 m

3. If any of the axes are perpendicular to a mirror plane we put a slash (/) between the symbol for the axis and the symbol for the mirror plane.  In this case, each of the 2-fold axes are perpendicular to mirror planes, so our symbol becomes:

2/m2/m2/m

If you look  in the table given in the lecture notes below, you will see that this crystal model belongs to the Rhombic-dipyramidal class.

2

Each of the mirror planes is unique.  We can tell that because each one cuts a different looking face.  So, we write 2 "m"s, one for each mirror plane:

2 m m

2mm

For this crystal class, the convention is to write mm2 rather than 2mm (I'm not sure why).  If you consult the table below, you will see that this crystal model belongs to the Rhombic-pyramidal class.

4  2  2

4/m2/m2/m

Looking in the table below, we see that this crystal belongs to the Ditetragonal-dipyramidal class.

4    2

There are 3 mirror planes that are perpendicular to the 4 fold axes, and 6 mirror planes that are perpendicular to the 2-fold axes.  No mirror planes are perpendicular to the 3-fold rotoinversion axes.  So, our final symbol becomes:

4/m2/m

Consulting the table in the lecture notes below, reveals that this crystal belongs to the hexoctahedral crystal class.

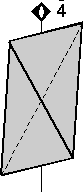
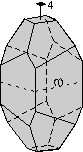
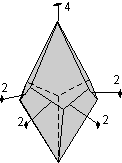
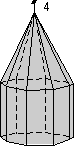
The 32 Crystal Classes

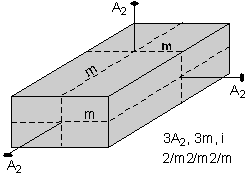
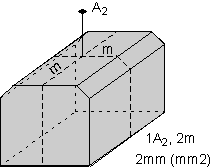
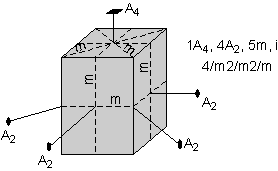
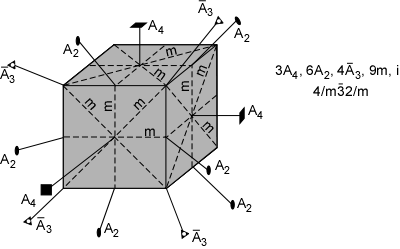
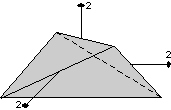
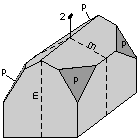
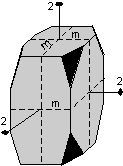
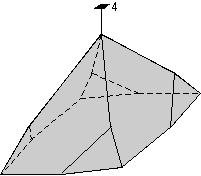
The 32 crystal classes represent the 32 possible combinations of symmetry operations.  Each crystal class will have crystal faces that uniquely define the symmetry of the class.  These faces, or groups of faces are called crystal forms.  Note that you are not expected to memorize the crystal classes, their names, or the symmetry associated with each class.  You will, however, be expected to determine the symmetry content of crystal models, after which you can consult the tables in your textbook, lab handouts, or lecture notes.  All testing on this material in the lab will be open book.

In this lecture we will go over some of the crystal classes and their symmetry.  I will not be able to cover all of the 32 classes.  You will, however, see many of the 32 classes during your lab work.  Note that it is not easy to draw a crystal of some classes without adding more symmetry or that can be easily seen in a two dimensional drawing.  

The table below shows the 32 crystal classes, their symmetry, Hermann-Mauguin symbol, and class name.
     

Note that the 32 crystal classes are divided into 6 crystal systems.

1. The Triclinic System has only 1-fold or 1-fold rotoinversion axes.
    
2. The Monoclinic System has only mirror plane(s) or a single 2-fold axis.
    
3. The Orthorhombic System has only two fold axes or a 2-fold axis and 2 mirror planes.
    
4. The Tetragonal System has either a single 4-fold or 4-fold rotoinversion axis.
    
5. The Hexagonal System has no 4-fold axes, but has at least 1 6-fold or 3-fold axis.
    
6. The Isometric System has either 4 3-fold axes or 4 3-fold rotoinversion axes.

Triclinic System

Characterized by only 1-fold or 1-fold rotoinversion axis

• Pedial Class,   1, Symmetry content - none
  
  In this class there is no symmetry, so all crystal faces are unique and are not related to each other by symmetry.  Such faces are called Pedions, thus this is the Pedial Class.  Only a few rare minerals are in this class.

• Pinacoidal Class,  , Symmetry content - i
  
  Since in this class there is only a center of symmetry, pairs of faces are related to each other through the center.  Such faces are called pinacoids, thus this is the pinacoidal class.  Among the common minerals with pinacoidal crystals are: microcline (K-feldspar), plagioclase, turquoise, and wollastonite.

Monoclinic System

Characterized by having only  mirror plane(s) or a single 2-fold axis.

• Sphenoidal Class,  2, Symmetry content - 1A₂ 
  
  In this class there is a single 2-fold rotation axis.  Faces related by a 2-fold axis are called sphenoids, thus this is the sphenoidal class. Only rare minerals belong to this class.

• Domatic Class, m, Symmetry content - 1m
  
  This class has a single mirror plane.  Faces related by a mirror plane are called domes, thus this is the domatic class.  Only 2 rare minerals crystallize in this class.

•  Prismatic Class, 2/m. Symmetry content - 1A₂, m, i
  
  This class has a single 2-fold axis perpendicular to a single mirror plane.  This class has pinacoid faces and prism faces.  A prism is defined as 3 or more identical faces that are all parallel to the same line.  In the prismatic class, these prisms consist of 4 identical faces, 2 of which are shown in the diagram on the front of the crystal.  The other two are on the back side of the crystal. 

Characterized by having only two fold axes or a 2-fold axis and 2 mirror planes.

• Rhombic -disphenoidal Class, 222, Symmetry content - 3A₂
  
  In this class there are 3  2-fold axis and no mirror planes.  The 2-fold axes are all perpendicular to each other.  The disphenoid faces that define this group consist of 2 faces on top of the crystal and 2 faces on the bottom of the crystal that are offset from each other by 90^o.  Epsomite is the most common rare mineral of this class.

• Rhombic-pyramidal Class, 2mm (mm2), Symmetry content - 1A₂, 2m
  
  This class has two perpendicular mirror planes and a single 2-fold rotation axis.  Because it has not center of symmetry, the faces on the top of the crystal do not occur on the bottom.  A pyramid, is a set of 3 or more identical faces that intersect at a point.  In the case of the rhombic pyramid, these would be 4 identical faces, labeled p, in the diagram.  

Hemimorphite is the most common mineral with this symmetry.

• Rhombic-dipyramidal Class, 2/m2/m2/m, Symmetry content - 3A₂, 3m, i
  
  This class has 3 perpendicular 2-fold axes that are perpendicular to 3 mirror planes.  The dipyramid faces consist of 4 identical faces on top and 4 identical faces on the bottom that are related to each other by reflection across the horizontal mirror plane or by rotation about the horizontal 2-fold axes.
  
  The most common minerals in this class are andalusite, anthophyllite, aragonite, barite, cordierite, olivine, sillimanite, stibnite, sulfur, and topaz.

Characterized by a single 4-fold or 4-fold rotoinversion axis.

• Tetragonal-pyramidal Class, 4, Symmetry content - 1A₄
  
  Since this class has a single 4-fold axis and no mirror planes, there are no pyramid faces on the bottom of the crystal.  Wulfinite is the only mineral known to crystallize in this class.
  
  
  
  

• Tetragonal-disphenoidal Class, , Symmetry content - 1₄
  
  With only a single 4-fold rotoinversion axis, the disphenoid faces consist of two identical faces on top, and two identical faces on the bottom, offset by 90^o.  Note that there are no mirror planes in this class.  Only one rare mineral is known to form crystals of this class.

• Tetragonal-dipyramidal Class, 4/m, Symmetry content - 1A₄, 1m, i
  
  This class has a single 4-fold axis perpendicular to a mirror plane.  This results in 4 pyramid faces on top that are reflected across the mirror plane to form 4 identical faces on the bottom of the crystal.  Scheelite and scapolite are the only common minerals in this class.
  

• Tetragonal-trapezohedral Class, 422, Symmetry content - 1A₄, 4A₂
  
  This class has a 4 fold axis perpendicular to 4 2-fold axes.  There are no mirror planes.  Only one rare mineral belongs to this class.

• Ditetragonal-pyramidal Class, 4mm, Symmetry content - 1A₄, 4m
  
  This class has a single 4-fold axis and 4 mirror planes.  The mirror planes are not shown in the diagram, but would cut through the edges and center of the faces shown.  Note that the ditetragonal pyramid is a set of 8 faces that form a pyramid on the top of the crystal. Only one rare mineral forms in the crystal class.
  
  

• Tetragonal-scalenohedral Class, 2m, Symmetry Content - 1₄, 2A₂, 2m
  
  This class has a 4-fold rotoinversion axis that is perpendicular to 2 2-fold rotation axes.  The 2 mirror planes a parallel to the and are at 45^o to the 2-fold axes.  Chalcopyrite and stannite are the only common minerals with crystals in this class.
  
  

• Ditetragonal-dipyramidal Class, 4/m2/m2/m, Symmetry content - 1A₄, 4A₂, 5m, i
  
  This class has the most symmetry of the tetragonal system.  It has a single 4-fold axis that is perpendicular to 4 2-fold axes.  All of the 2-fold axes are perpendicular to mirror planes.  Another mirror plane is perpendicular to the 4-fold axis.  The mirror planes are not shown in the diagram, but would cut through all of the vertical edges and through the center of the pyramid faces.  The fifth mirror plane is the horizontal plane.  Note the ditetragonal-dipyramid consists of the 8 pyramid faces on the top and the 8 pyramid faces on the bottom.  

Common minerals that occur with this symmetry are anatase, cassiterite, apophyllite, zircon, and vesuvianite.

Examples of questions on this material that could be asked on an exam

1. Why are there only 32 classes of crystals?
   
   
2. What criteria is involved in dividing the 32 crystal classes into 6 crystal systems?
   
   
3. Note that exams where you will be asked to recognize the different crystal classes and their symmetry, the exams will be open book, so you will have access to the tables and figures in these notes.
   

Return to EENS 2110 Page