| EENS 2110 | Mineralogy |
| Tulane University |
Prof. Stephen A. Nelson |
|
Properties of Light and Examination of Isotropic Substances |
|
|
|
| The optical properties of crystals are, next to x-ray diffraction and
direct chemical analyses, the most reliable properties available to
distinguish and identify minerals. The optical properties depend on the
manner that visible light is transmitted through the crystal, and thus are
dependent on crystal structure, crystal symmetry, and chemical composition
of the mineral.
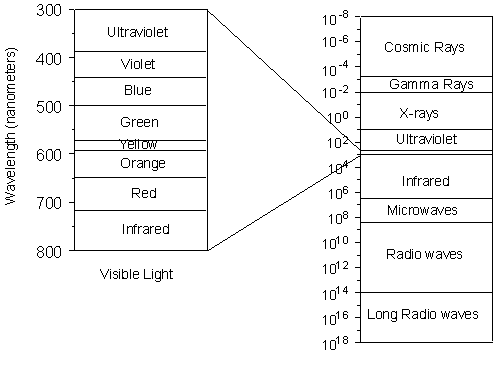
In order to understand the optical properties of crystals we must first understand something about light and how it interacts with matter. Light Light is electromagnetic radiation that has properties of waves. The electromagnetic spectrum can be divided into several bands based on the wavelength. As we have discussed before, visible light represents a narrow group of wavelengths between about 380 nm and 730 nm. |
|
|
| Our eyes interpret these wavelengths as different colors. If only
a single wavelength or limited range of wavelengths are present and enter
our eyes, they are interpreted as a certain color. If a single
wavelength is present we say that we have monochromatic light.
If all wavelengths of visible light are present, our eyes interpret this
as white light. If no wavelengths in the visible range are present,
we interpret this as dark.
Interaction of Light with Matter Velocity of Light and Refractive Index The energy of light is related to its frequency and velocity as follows: E = hν = hC/λ
where E = energy
The velocity of light, C, in a vacuum is 2.99793 x 1010cm/sec. Light cannot travel faster than this, but if it travels through a substance, its velocity will decrease. Note that from the equation given above- C = νλ The frequency of vibration, ν, remains constant when the light passes through a substance. Thus, if the velocity, C, is reduced on passage through a substance, the wavelength, λ, must also decrease. We here define refractive index, n, of a material or substance as the ratio of the speed of light in a vacuum, C, to the speed of light in a material through which it passes, Cm.
n = C/Cm Note that the value of refractive index will always be greater than 1.0, since Cm can never be greater than C. In general, Cm depends on the density of the material, with Cm decreasing with increasing density. Thus, higher density materials will have higher refractive indices. The refractive index of any material depends on the wavelength of light because different wavelengths are interfered with to different extents by the atoms that make up the material. In general refractive index varies linearly with wavelength. Materials can be divided into 2 classes based on how the velocity of light of a particular wavelength varies in the material.
Air, since it is a gas, is isotropic. The refractive index of air is usually taken as 1.0, although its true value is 1.0003. |
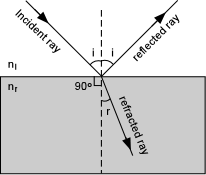
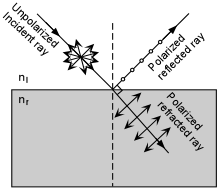
| Reflection and Refraction of Light
When light strikes an interface between two substances with different refractive indices, two things occur. An incident ray of light striking the interface at an angle, i, measured between a line perpendicular to the interface and the propagation direction of the incident ray, will be reflected off the interface at the same angle, i. In other words the angle of reflection is equal to the angle of incidence. |
| If the second substance is transparent to light, then a ray of light
will enter the substance with different refractive index, and will be
refracted, or bent, at an angle r, the angle of refraction. The
angle of refraction is dependent on the angle of incidence and the
refractive index of the materials on either side of the interface
according to Snell's Law:
Note that if the angle of incidence is 0o (i.e. the light enters perpendicular to the interface) that some of the light will be reflected directly back, and the refracted ray will continue along the same path. This can be seen from Snell's law, since sin(0o) = 0, making sin (r) = 0, and resulting in r = 0. |
 |
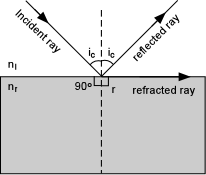
There is also an angle, ic, called the critical angle for total internal reflection where the refracted ray travels along the interface between the two substances. |
| This occurs when the angle r = 90o. In this case,
applying Snell's law:
ni sin (ic) = nr sin (90o)
= nr [since sin (90o) = 1] |
 |
| Dispersion of Light
The fact that refractive indices differ for each wavelength of light produces an effect called dispersion. This can be seen by shining a beam of white light into a triangular prism made of glass. White light entering such a prism will be refracted in the prism by different angles depending on the wavelength of the light. |
| The refractive index for longer wavelengths (red) are lower than those for shorter wavelengths (violet). This results in the a greater angle of refraction for the longer wavelengths than for the shorter wavelengths. (Shown here are the paths taken for a wavelength of 800 nm, angle r800 and for a wavelength of 300 nm, angle r300 ). When the light exits from the other side of the prism, we see the different wavelengths dispersed to show the different colors of the spectrum. | 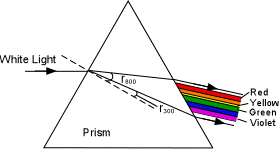 |
| Absorption of Light
When light enters a transparent material some of its energy is dissipated as heat energy, and it thus looses some of its intensity. When this absorption of energy occurs selectively for different wavelengths of light, they light that gets transmitted through the material will show only those wavelengths of light that are not absorbed. The transmitted wavelengths will then be seen as color, called the absorption color of the material. |
| For example, if we measure the intensity of light, Io, for each wavelength before it is transmitted through a material, and measure the intensity, I, for each wavelength after it has passed through the material, and plot I/Io versus wavelength we obtain the absorption curve for that material as shown here. The absorption curve (continuous line) for the material in this example shows that the light exiting the material will have a yellow-green color, called the absorption color. An opaque substance would have an absorption curve such as that labeled "Dark", i.e. no wavelengths would be transmitted. |
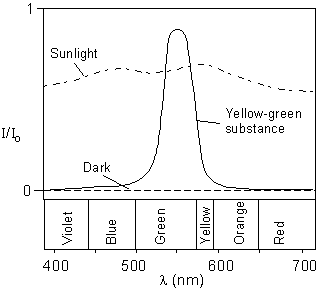 |
| Sunlight, on passing through the atmosphere has absorption curve as shown, thus we see it as white light, since all wavelengths are present. |
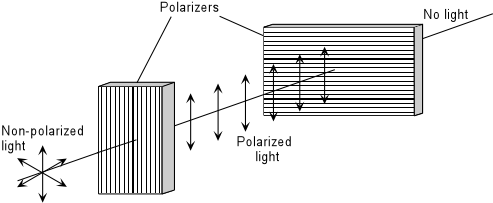
Polarization of Light Normal light vibrates equally in all direction perpendicular to its path of propagation. If the light is constrained to vibrate in only on plane, however, we say that it is plane polarized light. The direction that the light vibrates is called the vibration direction, which for now will be perpendicular to the direction. There are two common ways that light can become polarized. |
|
 |
|
 |
|
If a beam on non-polarized light encounters a polarizer, only light vibrating parallel to the polarizing direction of the polarizer will be allowed to pass. The light coming out on the other side will then be plane polarized, and will be vibrating parallel to the polarizing direction of the polarizer. If another polarizer with its polarization direction oriented perpendicular to the first polarizer is placed in front of the beam of now polarized light, then no light will penetrate the second polarizer. In this case we say that the light has been extinguished. |
|
Polaroid sunglasses use these same principles. For example,
incoming solar radiation is reflected off of the surface of the ocean or
the painted hood of your car. Reflected light coming off of either
of these surfaces will be polarized such that the vibration directions are
parallel to the reflected surface, or approximately horizontal (as in the
first method of polarization discussed above). Polaroid sunglasses
contain polarizers with the polarization direction oriented
vertically. Wearing such glasses will cut out all of the
horizontally polarized light reflecting off the water surface or hood of
your car. |
|
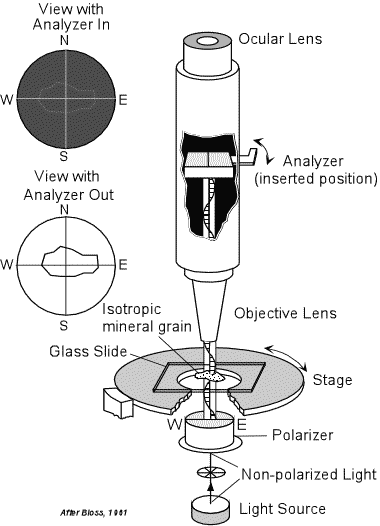
The Polarizing Microscope In optical mineralogy we use a microscope called a polarizing microscope. Such a microscope is equipped with two polarizers that are normally oriented so that their polarization directions are perpendicular to one another. |
| Light from a light source located below the tube and stage of the
microscope is initially unpolarized. This light first passes through
the lower polarizer (usually just called the polarizer), where it becomes
polarized such that the light is vibrating from the users right to
left. These directions are referred to as East (right and West
(left). The light then passes through a hole in the rotatable stage
of the microscope and enters the lower lens, called the objective
lens.
Mounted within the microscope tube is a second polarizer, called the analyzer, that can be rotated or pushed so that in can be in the light path (inserted position) or not in the light path (analyzer out position). The analyzer has a polarization direction exactly perpendicular to that of the lower polarizer These directions are usually referred to as North - South. If the analyzer is in, then the plane polarized light coming from the lower polarizer will be blocked, and no light will be transmitted though the ocular lens above. |
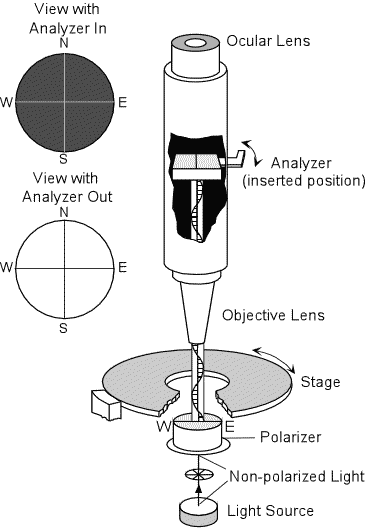 |
| If the analyzer is out, so that it is not in the light path, then the
polarized light will be transmitted through the ocular lens.
Next time we will see how this microscope is used to examine isotropic substances and determine their refractive indices. |
|
Isotropic Substances As discussed above, isotropic substance are those wherein the velocity of light or the refractive index does not vary with direction in the substance. Substances such as gases, liquids, glasses, and minerals that crystallize in the isometric crystal system are isotropic. We here introduce the concept of the optical indicatrix then look at what we see when we look at isotropic substances through the polarizing microscope. We then see how to determine the refractive index of isotropic substances as a means to identify them, and then take a first look at uniaxial materials.
The Isotropic Indicatrix The concept of the optical indicatrix is important as a visual means of looking at the way refractive index varies with direction in a substance. For isotropic minerals and substances the indicatrix is pretty trivial, since the refractive index does not vary with direction. |
| The optical indicatrix is simply a three dimensional object constructed by drawing vectors of length proportional to the refractive index for light vibrating parallel to the vector direction from a central point. The ends of all of the vectors are then connected to form the indicatrix. For isotropic minerals the indicatrix is a sphere as can be seen here. The indicatrix can be placed anywhere within or on a crystal so long as the crystallographic directions in the indicatrix are moved parallel to themselves. Again, for the isotropic indicatrix, this is fairly trivial since the refractive indices do not correspond to crystallographic directions and the refractive indices are the same in all directions, but the usefulness of the indicatrix concept will become much more clear when we look at anisotropic substances. |  |
|
Isotropic Substances and Polarized Light As discussed last time, the polarizing microscope has two
polarizers. The lower polarizer (often just called the polarizer) is
above the light source, and thus creates polarized light that vibrates in
the East West direction. The upper polarizer, called the analyzer,
is polarized to create polarized light vibrating at 90o to that
produced by the lower polarizer. Thus, if there is only air, an
isotropic substance, between the two polarizers, the E-W vibrating light
is completely eliminated at the analyzer, and no light passes through the
ocular lens. Isotropic substances do not change the vibration
direction of light as the light passes through the substance. |
| So, if we place a mineral grain on a glass slide (glass is also
isotropic), and view the grain through the ocular lens with the analyzer
not inserted in the light path, we will be able to clearly see the
grain. If the grain selectively absorbs light of certain
wavelengths, then the grain will show its absorption
color.
If we now insert the analyzer in the light path, the light coming out of the grain will still be polarized in an E-W direction, since isotropic substances do not change the polarization direction, and the analyzer will cut out all of this light. Thus, no light coming out of the mineral grain will pass through the analyzer. The mineral is thus said to be extinct in this position. Similarly, if we rotate the stage of the microscope, and thus rotate the grain, it will remain extinct for all rotation positions. (of course this is also true for the glass slide on which the grain rests, since glass is also isotropic). |
 |
| This is the primary means to determine whether or not a substance is isotropic. That is, rotate the grain on the microscope stage with the analyzer inserted. If the grain remains extinct throughout a 360o rotation of the stage, then the mineral or substance on the microscope stage is probably isotropic. |
|
Determination of Refractive Index for Isotropic Solids:The Immersion Method In isotropic substances, there are only two optical properties that can be determined. One of these is the absorption color, as discussed above. The other is the refractive index. Tables of refractive indices for isotropic minerals, list only the refractive index for one wavelength of light. The wavelength chosen is 589 nm, which corresponds to a yellow color. Such a wavelength would be given off of a sodium vapor lamp. Since these are expensive and generate much heat, sodium vapor lamps are not generally used in optical mineralogy. Instead we use white light. Still, as we shall see later, we can determine the refractive index for 589 nm. The determination of the refractive index of an isotropic substance is made by making a comparison with a substance of known refractive index. The comparison materials used are called refractive index oils. These are smelly organic oils that are calibrated over a range of refractive indices from 1.430 to 1.740 at intervals of 0.005. As you will see in lab, grains of the unknown substance are placed on a glass slide, a cover glass is placed over the grains, and a refractive index oil is introduced to completely surround the grains. This is called the immersion method. |
| The grains are then observed with the analyzer not inserted. If the grain has a refractive index that is very much different from the refractive index of the oil, then the grain boundaries will stand out strongly next to the surrounding oil. The grain will then be said to show high relief relative to the oil. High relief indicates that the refractive index of the grain is very much different from the refractive index of the oil. It does not tell us if the refractive index of the grain is less than or greater than the oil. | 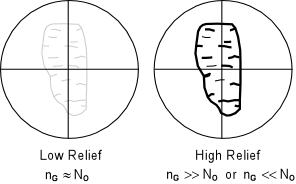 |
| If the refractive index of the grain and the oil are closer, then the
outline of the grain will not stand out as much from the oil. In
this case, the grain is said to low relief
relative to the oil. Again, low relief only indicates that the grain
and oil have similar refractive indices, and does not indicate that
the grain as a lower or higher refractive index than the oil.
If the refractive index of the grain is exactly the same as the refractive index of the oil, the boundaries of the grain will not be visible. That is to say that the grain will completely disappear in the oil. In this case the grain is said to have no relief relative to the oil. In order to determine whether the grain or the oil has a higher refractive index, a method called the Becke Line Method is used. The Becke Line Method A grain surrounded by oil when viewed through the microscope focused slightly above the position of sharpest focus will display two lines, one dark and one bright that concentric with the border of the grain. The brighter of these lines is called the Becke line and will always occur closest to the substance with a higher refractive index. This can be used to determine if the grain or the oil has the higher refractive index. |
| To use this method, one first focuses the microscope as sharply as
possible on the grain of interest. It is also useful to use the iris
diaphragm to cut down the incoming light as much as possible. This
will make the Becke line stand out better. Then using the fine
focus dial adjustment the microscope stage is lowered (or the objective
lens is raised) slightly out of focus. During this increase in focal
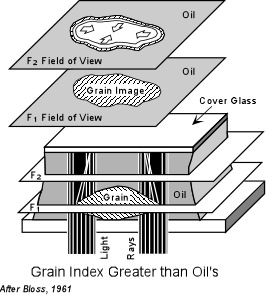
distance one observes a moving bright Becke line. If the Becke line
moves inward, the refractive index of the grain is greater than the
refractive index of the oil.
It is important to remember that the Becke line test is performed by increasing the distance between the grain and the objective lens. Thus, you should not memorize which way to turn the focusing knob, because it may be different with different brands of microscopes. |
 |
| Note also that if the focal distance is decreased, rather than increased, then the opposite results will be obtained, that is with decreasing focal distance the bright Becke line will move into the substance with lower refractive index. |
| For a grain with a refractive index less than that of the oil, the
opposite effect will be observed. When raising the objective lens or
lowering the stage so that the grain goes slightly out of focus, if the
bright Becke line moves into the oil, then the oil has a refractive index
greater than that of the grain.
This method can thus be used to start to narrow down the refractive index of the grain. For example, lets say that we first put grains of an unknown mineral in an oil with a refractive index of 1.540. In this oil, let's say the Becke line test shows that the oil has a higher refractive index than the grain. We could then choose for our next test to put the unknown grains in an oil with a lower refractive index. If the relief is very high, then we would know to choose an oil with a much smaller refractive index. |
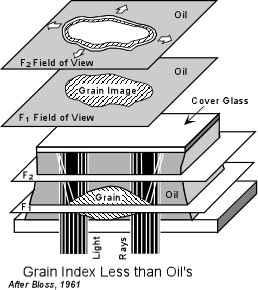 |
| Thus, by performing several tests in several different oils, we could
eventually find an oil that has a refractive index that exactly matches
that of the grain. In such a case the grain would have no relief
relative to the oil and would thus disappear in the oil.
But, this would not necessarily be true of the Becke lines. Recall from above that we said that refractive indices for grains (and also oils) are reported for a specific wavelength of light. That wavelength is 589 nm, which corresponds to yellow. Since we are using white light as an illuminator for our grain, the Becke line will be different for different wavelengths or colors of light. |
| This can be seen by examination of dispersion chart, as shown here. This is simply a plot of refractive index versus wavelength. Typical oils used in optical mineralogy generally show a dispersion curve with a steeper slope than that of minerals. Thus, when we have an exact match of refractive index between the grain and the oil for yellow light, we will still see a orange to red colored Becke line that will be move into the grain, and blue to violet colored Becke line that will move into the oil. | 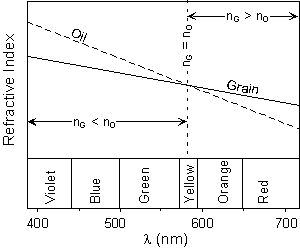 |
| One other property we can determine for all minerals (including anisotropic minerals) is cleavage or fracture. This can be seen because it is usually necessary to crush or break minerals to obtain a size suitable for mounting in oils. This property can best be seen with the analyzer not inserted. |
| Minerals or glasses that show concoidal fracture will have curved grain boundaries. If a single cleavage direction is present, then it will show as parallel grain boundaries. Sometimes, the cleavages can be seen as breaks within a grain as well, although this is more common in thin sections than in grain mounts. Two cleavage directions will show as intersecting straight sided grain boundaries. Three or more cleavage directions should be visible as well, but it must be remembered that the microscope view is nearly 2-dimensional, so you may be able to see only 2 cleavage directions at once. | 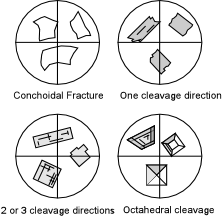 |
Summary of Observations of Isotropic Minerals
Next time we will look at the class of anisotropic minerals called uniaxial minerals. |
Examples of questions on this material that could be asked on an exam
|