| EENS 2110 |
Mineralogy |
| Tulane University |
Prof. Stephen A. Nelson |
|
X-Ray Crystallography |
|
|
|
| Prior to the discovery of X-rays by Conrad Roentgen in 1895,
crystallographers had deduced that crystals are made of an orderly
arrangement of atoms and could infer something about this orderly
arrangement from measurements of the angles between crystal faces.
The discovery of X-rays gave crystallographers a powerful tool that could
"see inside" of crystals and allow for detailed determination of
crystal structures and unit cell size. Here we discuss the
application of X-rays, not so much in terms of how they are used to
determine crystal structure, but how they can be used to identify
minerals.
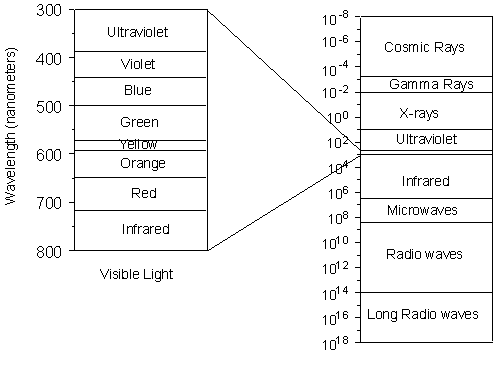
Nevertheless, we still need to know something about X-rays, how they are generated, and how they interact with crystalline solids. X-rays and the Production of X-rays X-rays are electromagnetic radiation with wavelengths between about 0.02 Å and 100 Å (1Å = 10-10 meters). They are part of the electromagnetic spectrum that includes wavelengths of electromagnetic radiation called visible light which our eyes are sensitive to (different wavelengths of visible light appear to us as different colors). Because X-rays have wavelengths similar to the size of atoms, they are useful to explore within crystals. |
|
| The energy of X-rays, like all electromagnetic radiation, is inversely
proportional to their wavelength as given by the Einstein equation:
E = hν = hc/λ
Thus, since X-rays have a smaller wavelength than visible light, they have higher energy. With their higher energy, X-rays can penetrate matter more easily than can visible light. Their ability to penetrate matter depends on the density of the matter, and thus X-rays provide a powerful tool in medicine for mapping internal structures of the human body (bones have higher density than tissue, and thus are harder for X-rays to penetrate, fractures in bones have a different density than the bone, thus fractures can be seen in X-ray pictures). |
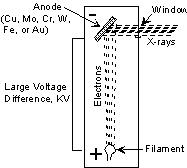
X-rays are produced in a device called an X-ray tube. Such a tube is illustrated here. It consists of an evacuated chamber with a tungsten filament at one end of the tube, called the cathode, and a metal target at the other end, called an anode. Electrical current is run through the tungsten filament, causing it to glow and emit electrons. A large voltage difference (measured in kilovolts) is placed between the cathode and the anode, causing the electrons to move at high velocity from the filament to the anode target. Upon striking the atoms in the target, the electrons dislodge inner shell electrons resulting in outer shell electrons having to jump to a lower energy shell to replace the dislodged electrons. These electronic transitions results in the generation of X-rays. The X-rays then move through a window in the X-ray tube and can be used to provide information on the internal arrangement of atoms in crystals or the structure of internal body parts. |
 |
|
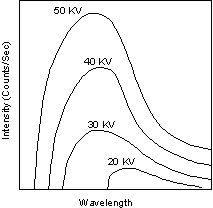
Continuous and Characteristic X-ray Spectra When the target material of the X-ray tube is bombarded with electrons accelerated from the cathode filament, two types of X-ray spectra are produced. The first is called the continuous spectra. |
| The continuous spectra consists of a range of wavelengths of X-rays with
minimum wavelength and intensity (measured in counts per second) dependent
on the target material and the voltage across the X-ray tube. The
minimum wavelength decreases and the intensity increases as voltage
increases.
The second type of spectra, called the characteristic spectra, is produced at high voltage as a result of specific electronic transitions that take place within individual atoms of the target material. |
 |
This is easiest to see using the simple Bohr model of the atom. In such a model, the nucleus of the atom containing the protons and neutrons is surrounded by shells of electrons. The innermost shell, called the K- shell, is surrounded by the L- and M - shells. When the energy of the electrons accelerated toward the target becomes high enough to dislodge K- shell electrons, electrons from the L - and M - shells move in to take the place of those dislodged.
|
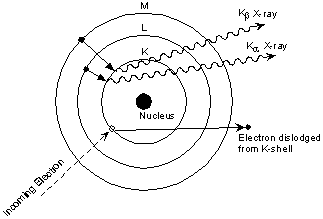 |
Each of these electronic transitions produces an X-ray with a wavelength that depends on the exact structure of the atom being bombarded. A transition from the L - shell to the K- shell produces a Kα X-ray, while the transition from an M - shell to the K- shell produces a Kβ X-ray.
|
| These characteristic X-rays have a much higher intensity than those produced by the continuous sprectra, with Kα X-rays having higher intensity than Kb X-rays. The important point here is that the wavelength of these characteristic x-rays is different for each atom in the periodic table (of course only those elements with higher atomic number have L- and M - shell electrons that can undergo transitions to produce X-rays). A filter is generally used to filter out the lower intensity Kβ X-rays. |  |
For commonly used target materials in X-ray tubes, the X-rays have the
following well-known experimentally determined wavelengths:
|
|
|
|
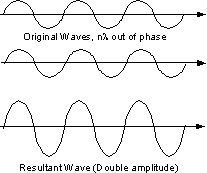 |
Since a beam of X-rays consists of a bundle of separate waves, the waves can interact with one another. Such interaction is termed interference. If all the waves in the bundle are in phase, that is their crests and troughs occur at exactly the same position (the same as being an integer number of wavelengths out of phase, nλ, ν = 1, 2, 3, 4, etc.), the waves will interfere with one another and their amplitudes will add together to produce a resultant wave that is has a higher amplitude (the sum of all the waves that are in phase. |
 |
If the waves are out of phase, being off by a non-integer number of wavelengths, then destructive interference will occur and the amplitude of the waves will be reduced. In an extreme case, if the waves are out of phase by an odd multiple of 1/2λ [(2n+1)/2λ ], the resultant wave will have no amplitude and thus be completely destroyed. |
| The atoms in crystals interact with X-ray waves in such a way as to produce interference. The interaction can be thought of as if the atoms in a crystal structure reflect the waves. But, because a crystal structure consists of an orderly arrangement of atoms, the reflections occur from what appears to be planes of atoms. Let's imagine a beam of X-rays entering a crystal with one of these planes of atoms oriented at an angle of θ to the incoming beam of monochromatic X-rays (monochromatic means one color, or in this case 1 discreet wavelength as produced by the characteristic spectra of the X-ray tube). |
| Two such X-rays are shown here, where the spacing between the atomic planes occurs over the distance, d. Ray 1 reflects off of the upper atomic plane at an angle θ equal to its angle of incidence. Similarly, Ray 2 reflects off the lower atomic plane at the same angle θ. While Ray 2 is in the crystal, however, it travels a distance of 2a farther than Ray 1. If this distance 2a is equal to an integral number of wavelengths (nλ), then Rays 1 and 2 will be in phase on their exit from the crystal and constructive interference will occur. | 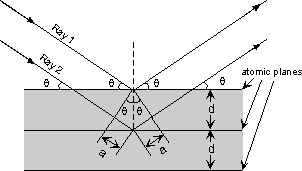 |
| If the distance 2a is not an integral number of wavelengths, then
destructive interference will occur and the waves will not be as strong as
when they entered the crystal. Thus, the condition for constructive
interference to occur is
nλ = 2a but, from trigonometry, we can figure out what the distance 2a is in terms of the spacing, d, between the atomic planes. a = d sin θ or 2a = 2 d sin θ thus, nλ = 2d sin θ This is known as Bragg's Law for X-ray diffraction. What it says is that if we know the wavelength ,λ , of the X-rays going in to the crystal, and we can measure the angle θ of the diffracted X-rays coming out of the crystal, then we know the spacing (referred to as d-spacing) between the atomic planes. d = nλ /2 sin θ Again it is important to point out that this diffraction will only occur if the rays are in phase when they emerge, and this will only occur at the appropriate value of n (1, 2, 3, etc.) and θ. In theory, then we could re-orient the crystal so that another atomic plane is exposed and measure the d-spacing between all atomic planes in the crystal, eventually leading us to determine the crystal structure and the size of the unit cell. |
|
The X-ray Powder Method In practice, this would be a time consuming operation to reorient the crystal, measure the angle θ, and determine the d-spacing for all atomic planes. A faster way is to use a method called the powder method. In this method, a mineral is ground up to a fine powder. In the powder, are thousands of grains that have random orientations. With random orientations we might expect most of the different atomic planes to lie parallel to the surface in some of the grains. Thus, by scanning through an angle θ of incident X-ray beams form 0 to 90o, we would expect to find all angles where diffraction has occurred, and each of these angles would be associated with a different atomic spacing. |
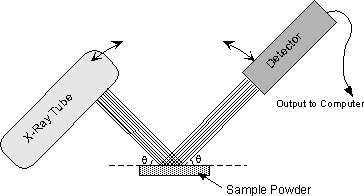 |
The instrument used to do this is an x-ray powder diffractometer. It consists of an X-ray tube capable of producing a beam of monochromatic X-rays that can be rotated to produce angles from 0 to 90o. A powdered mineral sample is placed on a sample stage so that it can be irradiated by the X-ray tube. To detect the diffracted X-rays, an electronic detector is placed on the other side of the sample from the X-ray tube, and it too is allowed to rotate to produce angles from 0 to 90o. |
The instrument used to rotate both the X-ray tube and the detector is called a goniometer. The goniometer keeps track of the angle θ, and sends this information to a computer, while the detector records the rate of X-rays coming out the other side of the sample (in units of counts/sec) and sends this information to the computer. |
| After a scan of the sample the X-ray intensity can be plotted against the angle θ (usually reported as 2θ because of the way older diffractometers were made) to produce a chart, like the one shown here. The angle 2θ for each diffraction peak can then be converted to d-spacing, using the Bragg equation. | 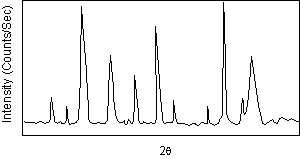 |
|
One can then work out the crystal structure and associate each of the
diffraction peaks with a different atomic plane in terms of the Miller
Index for that plane (hkl).
A group known as the Joint Committee on Powder Diffraction Standards (JCPDS) has collected data such as this on thousands of crystalline substances. This data can be obtained as the JCPDS Powder Diffraction File. Since every compound with the same crystal structure will produce an identical powder diffraction pattern, the pattern serves as kind of a "fingerprint" for the substance, and thus comparing an unknown mineral to those in the Powder Diffraction file enables easy identification of the unknown. We will see how this is done in our laboratory demonstration. |
Examples of questions on this material that could be asked on an exam
|