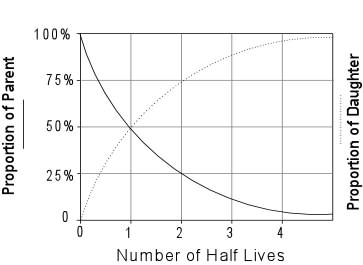
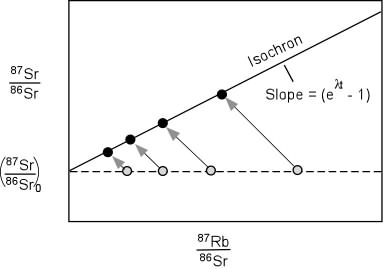
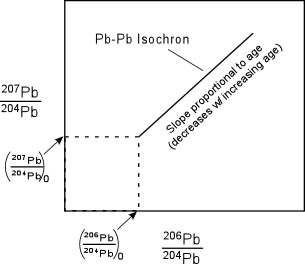
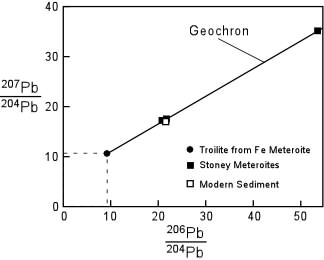
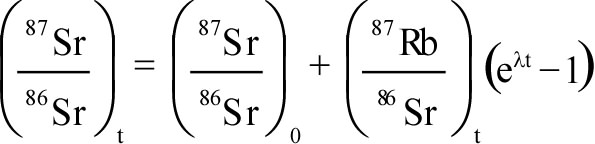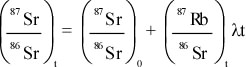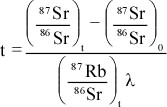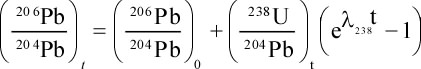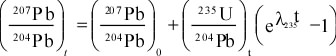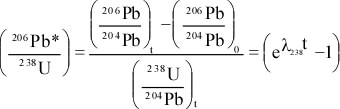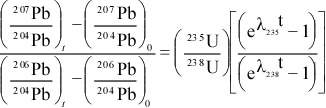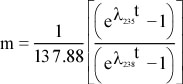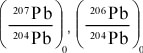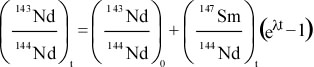- It provided another source of heat, not considered by Kelvin, which
would mean that the cooling time would have to be much longer.
- It provided a means by which the age of the Earth could be
determined independently.
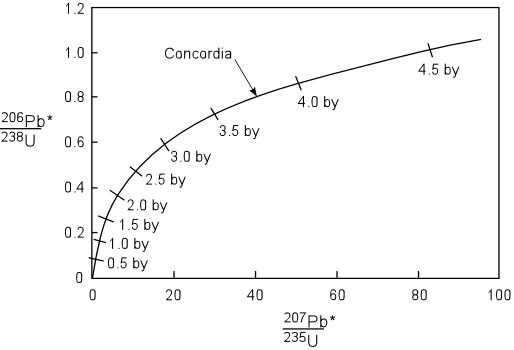
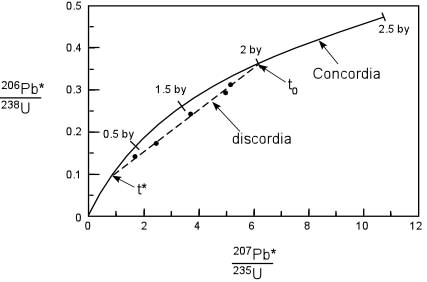
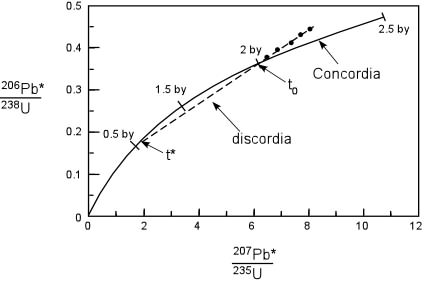
Principles of Radiometric Dating
Radioactive decay is described in terms of the probability that a constituent particle of the nucleus of an atom will escape through the potential (Energy) barrier which bonds them to the nucleus. The energies involved are so large, and the nucleus is so small that physical conditions in the Earth (i.e. T and P) cannot affect the rate of decay.
The rate of decay or rate of change of the number N of particles is proportional to the number present at any time, i.e.
![]()
Note that dN/dt must be negative.
The proportionality constant is λ, the decay constant. So, we can write
![]()
Rearranging, and integrating, we get
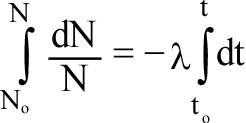
or
ln(N/No) = -λ(t - to)