1.Wavelets and sparse representations based signal processing
Given our multi-disciplinary background in mathematical sciences, signal and image processing, biomedical imaging and bioinformatics, the representation and analysis of biomedical imaging and genomic data have been our long interest. We first proposed the B-spline scale-space theory as an alternative to the widely used Gaussian scale-space approach in the area of computer vision and image processing research. The theory we proposed has several advantages over traditional methods. We also develop a differential wavelets, which can have faster computational efficiency, which have found widespread applications in signal and image processing.
a. Yu-Ping Wang, S. L. Lee, Scale-space derived from B-splines, IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 20, no. 10, Oct. 1998, pp.1050-1065.
b. Yu-Ping Wang, S. L. Lee, K. Torachi, Multiscale curvature based shape representation using B-spline wavelets, IEEE Trans. Image Processing, vol. 8, no 11, 1999. pp. 1586-1592.
c. Yu-Ping Wang, Image representations using multiscale differential operators, IEEE Trans. Image Processing, vol. 8, no. 12, 1999, pp. 1757-1771.
d. Yu-Ping Wang, Ruibin Qu. Fast implementation of scale-space by interpolatoy subdivision scheme, IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 21, no. 9, 1999 pp.1050-1065.
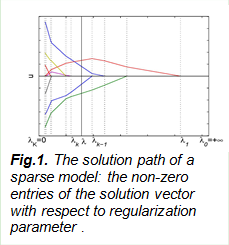
Our recent effort has been the development of sparse representation models, where we propose a theory on an easy condition to recover the sparse signals. A number of papers are currently under review.
e. J. Duan, C. Soussen, D. Brie, J. Idier and Y.-P. Wang, On LARS/homotopy equivalence conditions for over-determined LASSO, IEEE Signal Processing Letters, 19(12), 2012.
The representation and analysis of multi-scale and multi-modal biological data sets is ubiquitous but challenging in many disciplines. We have been working on sparse data representation method, a hot topic in both signal processing, statistics and applied mathematics. The field is more exciting within the context of big data science and technique, which are highly promoted by NIH and NSF, as demonstrated by several program announcements recently. This is especially the case with multi-omics data, where huge amounts of genomic data of different nature, format, organization and structure are produced at different genomic platforms and at multiple scales. These data sets provide rich and complementary information; how to represent and integrate these muli-omics data for systems biology study has become a promising and emerging research topic. We continue this line of research and apply to both imaging and genomic data analysis.

