| EENS 2120 |
Petrology |
| Tulane University |
Prof. Stephen A. Nelson |
|
Ternary Phase Diagrams |
|
Crystallization in Ternary Systems I. Equilibrium Crystallization Where all 2 Component Systems are Binary Eutectic Systems. |
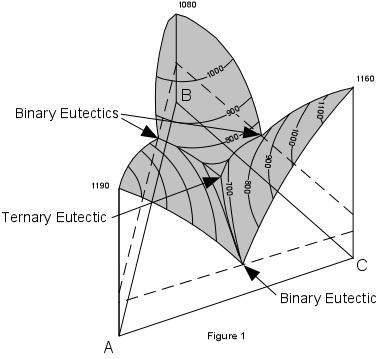
| Figure 1 shows a three dimensional representation of the three component (ternary) system ABC. Note that composition is measured along the sides of the basal triangle and temperature (or pressure) is measured vertically. The top of the figure shows a surface with contour's representing lines of constant temperature. These contours are called isotherms. Note that the eutectic points in each of the binary systems project into the ternary systems as curves. These curves are called boundary curves, and any composition on one of these curves will crystallize the two phases on either side of the curve. |  |
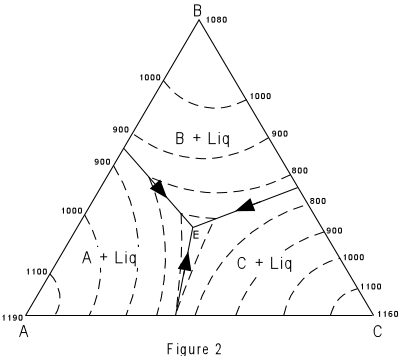
| Figure 2 shows the same figure in two dimensions as seen from above. The
boundary curves and isotherms are also shown projected onto the basal triangle. Note how
the temperature decreases toward the center of the diagram
In Figure 3 we trace the crystallization of composition X. Figure 3 is the same as Figure 2, with the isotherms left off for greater clarity. |
 |
| Note that the final solid must consist of crystals A + B + C since the initial
composition is in the triangle ABC.
At a temperature of about 980° the liquid of composition X would intersect the liquidus surface. At this point it would begin to precipitate crystals of C. As temperature is lowered, crystals of C would continue to precipitate, and the composition of the liquid would move along a straight line away from C. This is because C is precipitating and the liquid is becoming impoverished in C and enriched in the components A + B. |
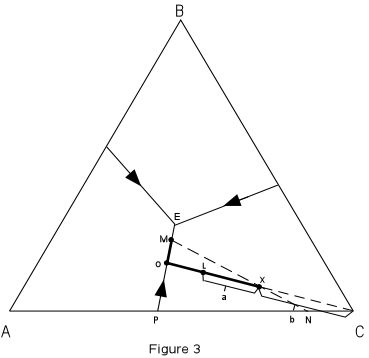 |
At a temperature of about 820°, point L in Figure 3, we
can determine the relative proportion of crystals and liquid.
With further cooling, the path of the liquid composition will intersect the boundary curve at point 0. At the boundary curve crystals of A will then precipitate. The liquid path will then follow the boundary curve towards point M. The bulk composition of the solid phase precipitated during this interval will be a mixture of A + C in the proportion shown by point P. At point M, the bulk composition of the solid phases so far precipitated through the cooling history lies at point N (the extension of the straight line from M through the initial composition X). At this time the % solid will be given by the distances :
and the % liquid by the distances:
Note, however, that the solid at this point consists of crystals of A and crystals of C. So, we must further break down the percentages of the solid. This is done as follows: The percentage of the solid that is A will be given by the distance from C to N relative to the distance between A and C; i.e. by the formula:
Similarly, the percentage of the solid consisting of crystals of C is given by the formula:
We can now calculate the exact percentage of all phases present in composition X at a temperature of 660° (where the liquid composition is at point M). The following formulae apply:
or
and
or
Note also that we can determine the composition of all phases present in the system at this point. The composition of the liquid is given by reading the composition of point M off the basal triangle. Since it is a mixture of A, B, and C, it will have a composition expressed in terms of the percentages of A, B, and C. The composition of the solids are 100%A and 100% C; i.e. they are pure solid phases (not mixtures). With further cooling, the liquid composition will move to the ternary eutectic, E, at a Temperature of about 650°, at which point crystals of B will precipitate. The temperature will remain constant until all of the liquid is used up. The final crystalline product will consist of crystals of A + B + C in the proportions given by the initial composition X. Crystallization will proceed in an analogous manner for all other compositions in the ternary system. To summarize, we can express the path of crystallization for composition X in an abbreviated form as follows:
|
|
 |
II. Crystallization in Ternary Systems that Contain a Compound that Melts Congruently. A ternary system that has a binary system with a compound that shows congruent melting (melts to a liquid of its own composition) is shown in Figure 5. Also shown is the binary system X-Y that contains the intermediate compound W. The result of the addition of this intermediate compound is essentially that the ternary system XYZ is divided into two smaller ternary systems represented by triangles WYZ and XWZ. |
| Crystallization in this system is illustrated in Figure 6, where the isotherms have been removed for simplicity. | |
| We first note that any composition within the triangle WYZ must end up
with crystals of W + Y + Z in the final crystalline product, compositions in the triangle
XWY will end up with crystals of X + W + Y, and compositions on the line WZ must end up
with crystals of W + Z only.
Consider first crystallization of composition A in Figure 6. Crystallization begins at about 1160° with separation of crystals of Z. The composition of the liquid then changes along a straight line away from Z. When the temperature reaches about 680°, the liquid composition has intersected the boundary curve at point B. |
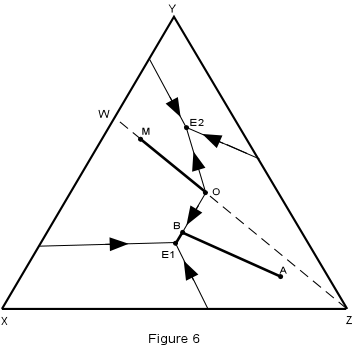 |
| At this time, crystals of W begin to separate and with further lowering of
temperature, the liquid moves along the boundary curve, B-E1, precipitating crystals of Z
+ W. When the liquid reaches the ternary eutectic, E1, crystals of X begin to separate
along with crystals of W and Z. The temperature remains constant at 640°
until all of the liquid is used up leaving a final product of crystals of X + W + Z in the
proportions of the original composition, A.
We can summarize this crystallization history in abbreviated form as follows:
|
| Now consider the crystallization of composition M which lies on the binary system W-Z. Since this is a binary system, only phases W and Z will be found in the final crystalline product. Thus, crystallization will stop when the liquid composition reaches the point O, which is equivalent to the binary eutectic in the system W-Z. |
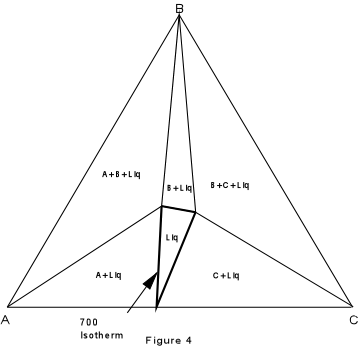
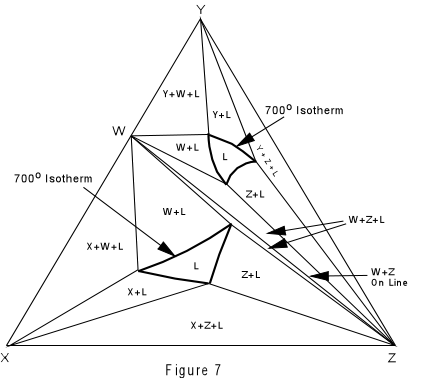
Again, we can construct isothermal planes showing the phases present in any part of the system at any temperature of interest. Such an isothermal plane at 700° for the system XYZ is shown in Figure 7. |
 |
III. Crystallization in Ternary Systems Containing an Incongruently Melting Compound. A. Equilibrium Crystallization |
We will consider equilibrium crystallization of compositions P, Q, S, T and X, as all
will behave somewhat differently.
|
B. Fractional Crystallization We next consider what might happen under conditions of fractional crystallization in the system. As you recall, fractional crystallization occurs when a crystalline phase is somehow removed from the system and is thus prevented from reacting with the liquid to form different crystals. Consider now fractional crystallization of composition P in Figure 8. Under equilibrium conditions, composition P would follow the path discussed above, becoming completely solid at the ternary peritectic, R, with an assemblage of crystals of A + D + C. |
| We will consider fractional crystallization in steps for this example. That is at
various points we will imagine all of the previously precipitated crystals are somehow
removed. At 1090° composition P begins to crystallize.
Crystals of A separate from the liquid. On cooling to point Q, we remove all of the
previously precipitated crystals of A, our system now has composition Q, since we have
removed part of the system that has already crystallized as crystals of A.
Cooling to point S, more crystals of A precipitate, and again are removed from the system. Note that at this point, the system has the composition S. Further cooling of composition S, without removing any more crystals from the system, would result in the liquid composition following the equilibrium crystallization path of composition S, as discussed above. Note that composition S is in the triangle D-C-B, and would end up crystallizing D, C, and B, in contrast to the assemblage that would have crystallized from composition P (A, D, and C) if it had crystallized under equilibrium conditions. Thus fractional crystallization of composition P would result in not only a different final crystalline assemblage, but a final liquid composition which is very different from the final liquid composition that would result from equilibrium crystallization. If we continue our fractional crystallization of composition P, starting with the liquid (and system) having a composition of S, further cooling to point T on the boundary curve, results in further precipitation of A. If we remove all crystals of A, the system now has a composition T. Because no crystals are present to react with the liquid to form crystals of D, the liquid composition will not change along the boundary curve towards R, but instead will move directly across the field where only D is precipitated. When the temperature reaches 680°, at point V, crystals of B form and the liquid composition changes along the boundary curve toward E. At E, crystals of C form and our final assemblage consists of crystals of D + B + C. Note how fractional crystallization has allowed the liquid to become enriched in B, while under equilibrium conditions no crystals of B could have formed. The system discussed above is very similar to the behavior of the system Mg2SiO4
- SiO2 - CaAl2Si2O8, where A = Forsterite, B =
Quartz, C = Anorthite, and D = Enstatite. Thus, knowledge of the crystallization behavior
of such a system is in many ways analogous to what may happen in magmas and shows how a
basaltic magma, that would normally only crystallize forsterite, enstatite, and
plagioclase, could change to a rhyolitic magma that would crystallize quartz.
|
| IV. Ternary System with a Binary Solid Solution. | |
| Figure 9 shows the ternary system Albite - Anorthite - Diopside. As you recall, albite and anorthite form a complete solid solution series (the plagioclase series). Anorthite and diopside form a eutectic system, as do albite and diopside. However, the eutectic in the system albite-diopside is very close to pure albite. The solid solution between albite and anorthite continues into the ternary system and is expressed by the boundary curve connecting the two binary eutectics. Note that this boundary curve forms a "temperature valley" in the ternary system. | 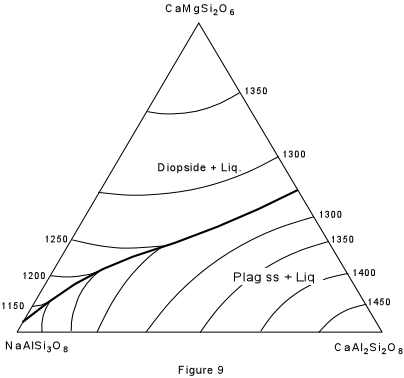 |
| We will now consider equilibrium crystallization of 2 compositions on the plagioclase side of the boundary curve. It must be noted that geometrical methods will not predict the exact path of equilibrium crystallization in systems of this type. We here give an approximate path consistent with experimental results. |
| First, consider crystallization of composition D, in Figure 10, which is
27% Albite, 46% Anorthite and 28% diopside. The final product should consist of pure
diopside and a plagioclase of composition 63% Anorthite.
At a temperature of about 1325° the liquid begins to crystallize with separation of plagioclase of composition 99% anorthite. As the liquid is cooled, it moves along the curved path D-P, while continually reacting with the previously precipitated plagioclase to form a more albitic plagioclase. |
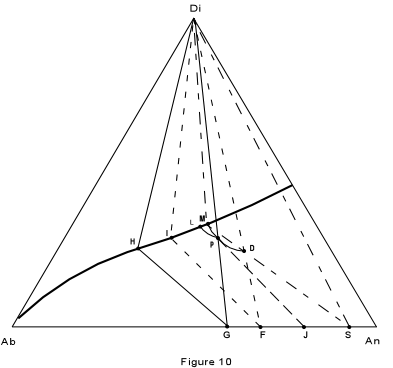 |
| By the time the liquid composition has reached point P, the Plagioclase has the
composition 98% anorthite. this is found by extending a line from the liquid composition
through the initial composition (D) back to the base of the triangle.
With continued cooling, the liquid composition will eventually reach the boundary curve at point M, at which time the plagioclase has the composition S (90% anorthite). We now construct what is known as a three phase triangle. It is shown in the figure by the straight line connecting the three phases in equilibrium, Di (solid), liquid (point M) and plagioclase solid solution (Point S). With continued cooling, the liquid composition changes along the boundary curve towards pure albite. Meanwhile the plagioclase solid solution is continually made over to more albitic compositions. Crystallization ceases when the base of the three phase triangle intersects the original liquid composition, D. Such a three phase triangle with apices Di, I, F, is shown in the figure. It indicates that the last liquid has the composition I, and is in equilibrium with pure diopside and a plagioclase composition of 70% anorthite (point F). Crystallization of composition P will be similar to that of D. Note, however that the liquid composition will follow a different path and intersect the boundary curve at point L. The liquid composition will then change along the boundary curve until the base of the three phase triangle Di, H, G, intersects the initial composition P. The final assemblage will then consist of pure diopside and plagioclase of composition G (60% anorthite). We now consider what would happen if the solid material were removed somehow, and prevented from reacting with the liquid. This is the case of fractional crystallization. Suppose we start again with composition D and cool it to a point where the liquid has the composition P. If we now remove all of the plagioclase that has crystallized up to this point, our liquid, and thus our entire system (without the removed crystals) now has the composition P. As we saw in the example above, composition P follows a different path of crystallization than composition D, and will produce a plagioclase of more albitic composition that of composition D. Thus, by continually removing plagioclase from contact with the liquid, it is possible, under perfect fractionation conditions to produce an almost pure albitic plagioclase from a liquid which would give a very calcic plagioclase under perfect equilibrium conditions. |
Examples of questions on this material that could be asked on an exam
|